Compare Two Numbers

How to Compare Two Numbers?

Here are some examples for comparison of numbers. Let us follow the rules to compare two numbers while solving the following questions.

When you compare two numbers and they are same then the numbers are equal and symbolized as (=).

i.e., When two numbers have the same value, we use the "=" sign ('equal to') to express the relationship between them.

For example,

218 = 218

Comparing two numbers means finding which number is smaller and which number is greater. It is represented by symbol (>) or (<).

When two numbers do not have the same value, we use the > sign ('greater than') or the < sign ('less than') depending on which number is on the left.

For example,

🔵 2321 is greater than 2231

2321 > 2231

🔵 2231 is less than 2321

2231-2321

Remember

The 'small' end of the signs, and <, always points to the smaller number.

75 > 70

70 < 75

Rules for Comparing Two Numbers:

1. First look at the digits in thousands place. The number with more number of thousands is a greater number.

2. When the digits in thousands place are equal, then the number with more number of hundreds is a greater number.

3. When the digits in hundreds place are equal, then the number with more number of tens is a greater number.

4. When the digits in tens place are equal, then the number with more number of ones is a greater number.

5. When all the digits are same, the numbers are equal.

I: Compare Two Numbers
When the Number of Digits are Different

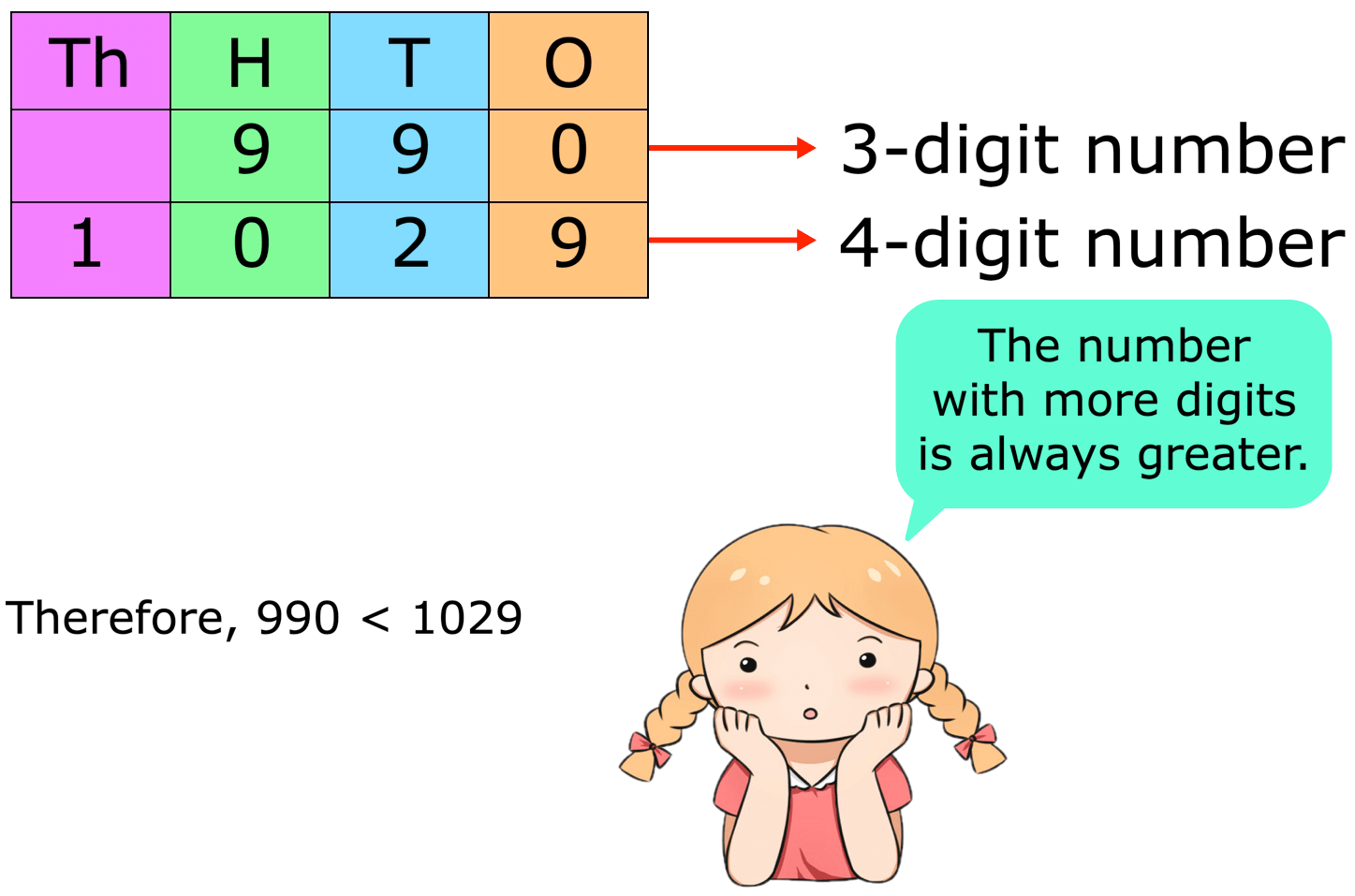
1. Compare 990 and 1029.

Solution:

I: Compare Two Numbers
When the Number of Digits are the Same.

(i) We compare the thousands first.

2. Compare which is greater 1539 or 3051?

Solution:

As      3 thousands > 1 thousands

So,     3051 > 1539.

(ii) If the digit in the thousands place is the same, compare the digits in the hundreds place.

3. Which is smaller 5643 or 5921?

Solution:

As   6 hundreds < 9 hundreds

So,  5643 < 5921

(iii) If the digits in the thousands place and the hundreds place are the same, compare the digits in the tens place.

4. Which one is greater 3754 or 3729?

Solution:

As   5 tens > 2 tens

So,  3754 > 3729

(iv) If the digits in the thousands place, the hundreds place and the tens place are the same, compare the digits in the ones place.

5. Which one is greater 2795 or 2798?

Solution:

As,   8 ones > 5 ones

So,   2798 > 2795

Solved Examples on Compare Two Numbers:

1. Which is greater and which is smaller:

(a) 345 or 94

Solution:

345 or 94

The number with more digits is greater than the number with lesser digits. The number 345 has 3 digits. The number 94 has 2 digits.

Hence, 345 > 94 or 94 < 345

(b) 3271 or 648

Solution:

3271 or 648 The number with more digits is greater than the number with lesser digits. The number 3271 has 4 digits. The number 648 has 3 digits.

Hence, 3271 > 648 or 648 < 3271 2.

This Video will demonstrate us the comparison between two numbers.

2. Compare two numbers:

(a) 4579 and 8271

Solution:

4579 and 8271 If two numbers have equal number of digits then the digits to the extreme left are compared. The one having the greater extreme left digit will be greater.

4579 and 8271 both have 4 digits.

But 8, the extreme left digit of 8271, is greater than 4, the extreme left digit of 4579. As 8 > 4

So, 8271 > 4579 or 4579 < 8271

(b) 973 and 879

Solution:

973 and 879

If two numbers have equal number of digits then the digits to the extreme left are compared. The one having the greater extreme left digit will be greater.

The digit 9 is greater than 8.

Hence, 973 > 879 or 879 < 973

3. Which is greater or smaller?

(a) 7934 or 7821

Solution:

7934 or 7821

If two numbers have equal number of digits and the first digit on the extreme left are equal, then their second digit from the extreme left are compared. The number having the greater second left digit is greater and so on.

7934 and 7821 both have first left digit equal, but second left digit 9 greater (>) than the other second left digit 8.

Hence, 7934 > 7821 or 7821 < 7934

(b) 5418 or 5462

Solution:

5418 or 5462

If two numbers have equal number of digits and the first digit on the extreme left are equal, then their second digit from the extreme left are compared. The number having the greater second left digit is greater and so on.

In 5418 and 5462, the first left digit 5 and second left digit 4 are equal. But in the ten’s place, 1 < 8

Hence, 5418 < 5462 or 5462 > 5418

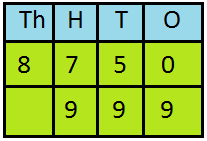
4. Compare 8750 and 999

Place the numbers one below the other. It will be easy to compare.

The given table shows that 8750 has 4-digits and 999 has only 3-digits. Therefore, 8750 is greater than 999.

Hence, 8750 > 999

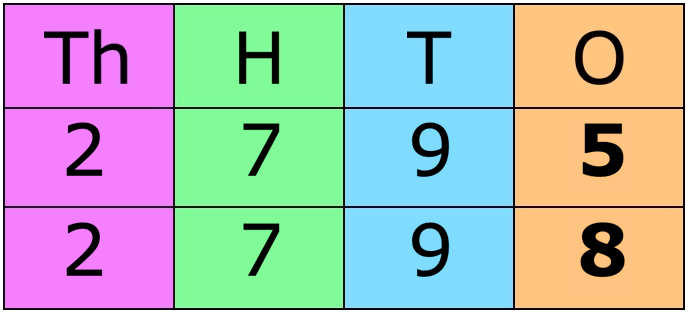
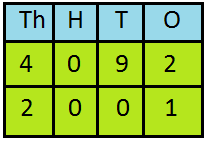
5. Compare 4092 and 2001

Place the numbers one below the other. It will be easy to compare.

Here, both the numbers have four digits. Compare the digits in the thousands place.

Since, 4 > 2

Hence, 4092 > 2001

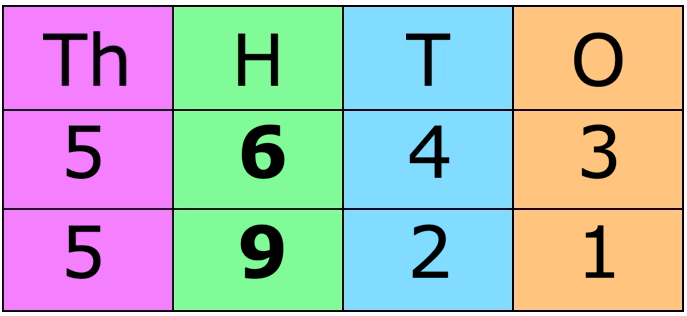
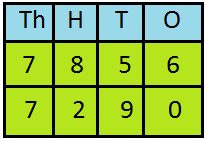
6. Compare 7856 and 7290

Place the numbers one below the other. It will be easy to compare.

Here, both the numbers have four digits and digits in thousands place is also same. Now, compare the digits in the hundreds place.

Since, 8 > 2

Hence, 7856 >7290

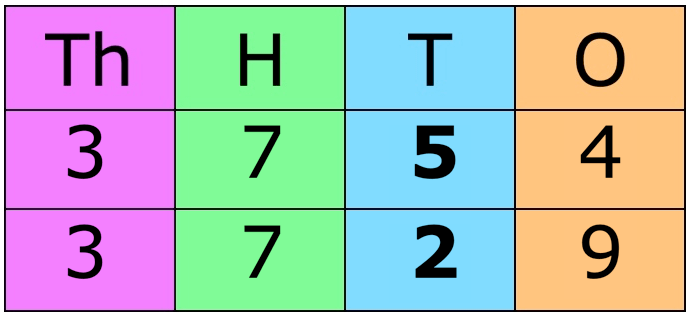
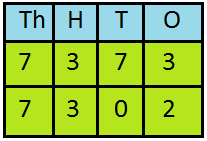
7. Compare 7373 and 7302

Place the numbers one below the other.

Here, both the numbers have four digits. Digits in thousands and hundreds places are same. Now, compare the digits in the tens place.

Since, 7 > 0

Hence, 7373 > 7302

The above worked-out problems on compare two numbers will help us to understand the rules for the comparison between two numbers.

3rd Grade Math Lessons

From Compare Two Numbers to HOME PAGE