Areas of Irregular Figures
Areas of irregular figures can be determined by dividing the figure into squares and rectangles.
Some irregular figures are made of rectangular or square regions. The areas of such irregular figures can be determined by calculating the areas of these rectangles and squares.
To find the area of a figure which is a combination of rectangles and a squares, we calculate the area of each figure separately and then add them to find total area.
Solved examples to find areas of irregular figures:
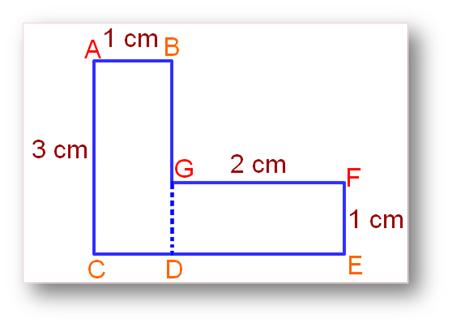
1. Find the area of the given figure:
Solution:
Area of a rectangle ABDC = 3 × 1
= 3 sq. cm.
Area of a rectangle EFGD = 2 × 1
= 2 sq. cm.
Therefore, Total Area = 3 + 2
= 5 sq. cm.
Area of the given figure = 5 sq. cm.
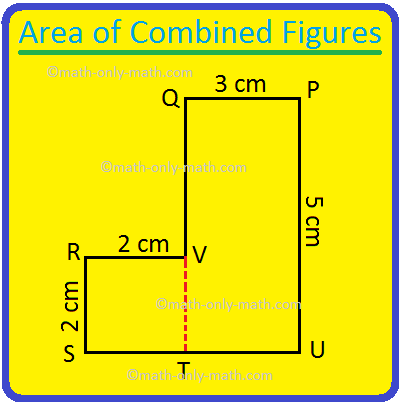
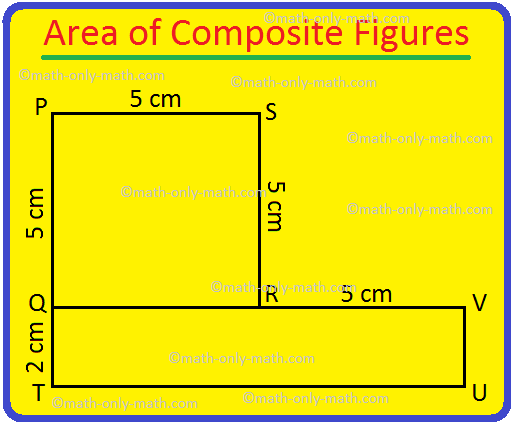
2. Find the area of the following figures.
Solution:
Area of the rectangle PQTU = 5 × 3 = 15 sq. cm.
Area of the square VRST = 2 × 2 = 4 sq. cm.
Total area of the figure = 15 + 4 = 19 sq. cm.
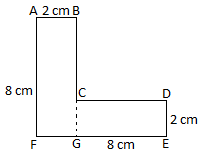
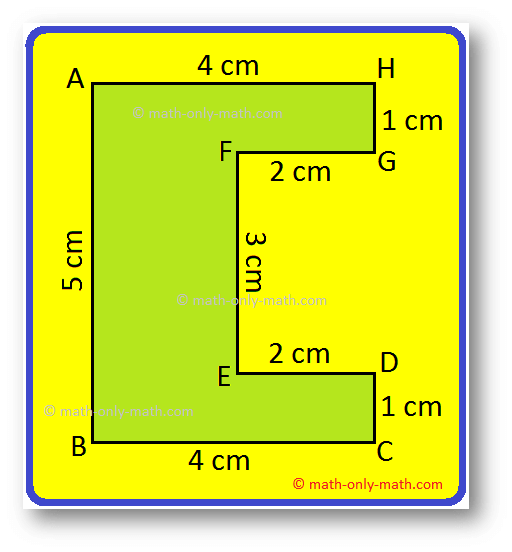
3. Find the area of the following figure.
Total area = Area of the rectangle ABGF + Area of the rectangle CDEG
= 8 × 2 cm\(^{2}\) + 2 × (8 - 2) cm\(^{2}\)
= 16 sq cm\(^{2}\) + 2 × 6 cm\(^{2}\)
= (16 + 12) cm\(^{2}\)
= 28 cm\(^{2}\)
Therefore, area of the figure = 28 cm\(^{2}\)
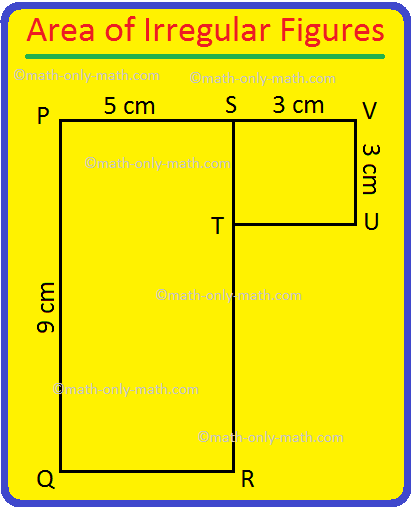
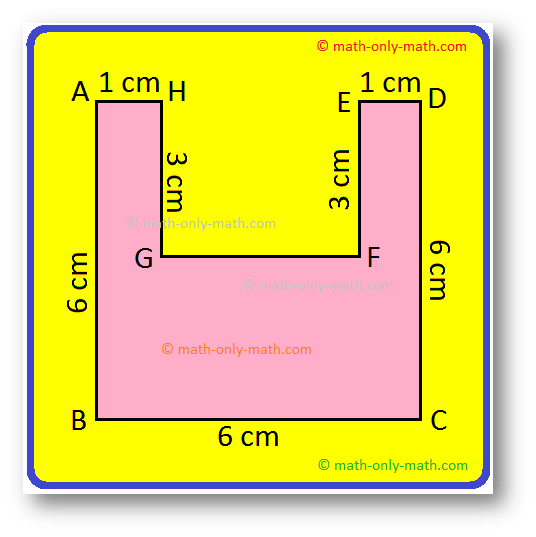
4. Find the area of the following figure.
(i) We divide the figure into two parts.
PQRS is a rectangle of length 9 cm and breadth 5 cm.
Area of PQRS = 9 × 5
= 45 sq. cm
STUV is a square of side 3 cm
Area of square STUV = 3 × 3 = 9 sq. cm
Hence, total area of the figure = 45 + 9 = 54 sq. cm
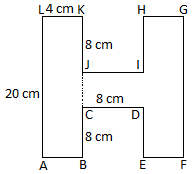
5. Find the area of the figure given on the right side.
Total area = Area of the rectangle ABKL + Area of the rectangle EFGH + Area of the rectangle CDIJ
= 20 × 4 cm\(^{2}\) + 20 × 4 cm\(^{2}\) + 8 × 4 cm\(^{2}\)
= 80 cm\(^{2}\) + 80 cm\(^{2}\) + 32 cm\(^{2}\)
= (80 + 80 + 32) cm\(^{2}\)
= 192 cm\(^{2}\)
Therefore, area of the figure = 192 cm\(^{2}\)
6. Find the area of the following figure.
Figure QTUV is a rectangle of length (5 cm + 5 cm = 10 cm) and breadth 2 cm
Area of QTUV = 10 × 2
= 20 sq. cm
PQRS is a square of side 5 cm
Area of PQRS = 5 × 5 = 25 sq. cm
Hence, total area of the figure = 20 + 25
= 45 sq. cm
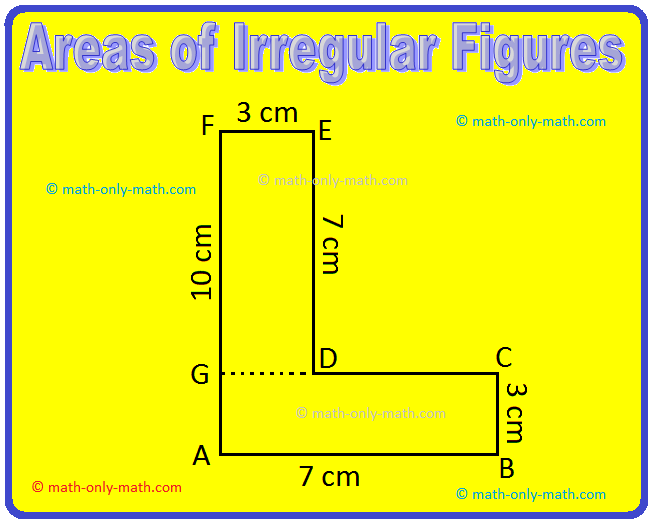
7. Find the area of the given irregular figure.
Solution:
Area of the rectangle DEFG
= ℓ x b
= 7 cm x 3 cm
= 21 cm²
Area of the rectangle ABCG
= ℓ x b
= 7 cm x 3 cm
= 21 cm²
Area of the complete figure = Area of rectangle DEFG + Area of rectangle ABCG
= 21 cm² + 21 cm²
= 42 cm²
Worksheet on Areas of Irregular Figures:
1. Find the area of the given irregular figure.
Answer:
1. 17.225 cm²
2. Find the area of the given irregular figure.
Answer:
2. 14 cm²
3. Find the area of the given figure.
Answer:
3. 24 cm²
You might like these
5th Grade Area and Perimeter Worksheet | With Answers | Free Worksheet
In 5th Grade Area and Perimeter Worksheet you will get different types of questions on perimeter of a triangle, perimeter of a square, perimeter of a rectangle, shapes of different kinds with the same perimeter, word problems on perimeter of a rectangle, word problems on
Perimeter and Area of Plane Figures | Definition of Perimeter and Area
A plane figure is made of line segments or arcs of curves in a plane. It is a closed figure if the figure begins and ends at the same point. We are familiar with plane figures like squares, rectangles, triangles and circles. Definition of Perimeter: The perimeter (P) of a
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find the perimeter of the triangles having the following sides.
Worksheet on Area and Perimeter of Rectangles | Word Problems |Answers
Recall the topic and practice the math worksheet on area and perimeter of rectangles. Students can practice the questions on area of rectangles and perimeter of rectangles. 1. Find the area and perimeter of the following rectangles whose dimensions are: (a) length = 17 m
Worksheet on Area | Test on Area | Home work on Area | Quiz on Area
In worksheet on area we will solve different types of question in area. 1. Find the area of a rectangle of length 24 cm and breadth 13 cm. 2. Find the area of a square of side 40 cm. 3. Find the area of a square of side 21 m.
Word Problems on Area and Perimeter | Free Worksheet with Answers
We will solve different types of word problems on area and perimeter. 1. The perimeter of a rectangular field is 260 m. If its length is 90 m, find its breadth.
Perimeter and Area of Irregular Figures | Solved Example Problems
Here we will get the ideas how to solve the problems on finding the perimeter and area of irregular figures. The figure PQRSTU is a hexagon. PS is a diagonal and QY, RO, TX and UZ are the respective distances of the points Q, R, T and U from PS. If PS = 600 cm, QY = 140 cm
Mental Math on Perimeter and Area | Maths Questions Answers
In mental math on perimeter and area we will solve different type of problems on perimeter of a triangle, perimeter of a square and a rectangle, area of a rectangle, area of a square and word problems on area.
Worksheet on Area of a Square and Rectangle | Area of Squares & Rectan
We will practice the questions given in the worksheet on area of a square and rectangle. We know the amount of surface that a plane figure covers is called its area. 1. Find the area of the square length of whose sides are given below: (i) 15 m (ii) 250 m (iii) 25 cm
Area of a Square | Area of a Square = (Side × Side) Square Units
In area of a square we will learn how to find the area by counting squares. To find the area of a region of a closed plane figure, we draw the figure on a centimeter squared paper and then count the number of squares enclosed by the figure. We know, that square is
Area of a Rectangle | Area of Rectangle = Length × Breadth | Examples
Area of a rectangle is discussed here. We know, that a rectangle has length and breadth. Let us look at the rectangle given below. Each rectangle is made of squares. The side of each square is 1 cm long. The area of each square is 1 square centimeter.
Area | Units to find Area | Conversion Table of Area | Two Dimensional
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed plane figures. In the following figures, the shaded region of each of the
● Area.
To find Area of a Rectangle when Length and Breadth are of Different Units.
To find Length or Breadth when Area of a Rectangle is given.
To find Cost of Painting or Tilling when Area and Cost per Unit is given.
To find the Number of Bricks or Tiles when Area of Path and Brick is given.
Worksheet on Area of a Square and Rectangle
5th Grade Math Problems
From Areas of Irregular Figures to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Subtraction of 4-Digit Numbers | Subtract Numbers with Four Digit
Jan 11, 25 03:35 PM
We will learn about the subtraction of 4-digit numbers (without borrowing and with borrowing). We know when one number is subtracted from another number the result obtained is called the difference. -
3rd Grade Addition Worksheet | 3-Digit Addition | Word Problems | Ans
Jan 11, 25 01:06 PM
In 3th Grade Addition Worksheet we will solve how to addition of 3-digit numbers without regrouping, addition of three 3-digit numbers without regrouping, addition of 3-digit numbers with regrouping… -
Addition of 4-Digit Numbers | 4-Digit Addition |Adding 4-Digit Numbers
Jan 11, 25 03:16 AM
We will learn about the addition of 4-digit numbers (without carrying and with carrying). We know how to add 2 or 3, 3-digit numbers without carrying or with carrying. -
Worksheet on Addition of 4-Digit Numbers | 4 Digit Addition Worksheets
Jan 11, 25 02:48 AM
Practice the questions given in the worksheet on addition of 4-digit numbers. Here we will add two 4-digit numbers (without carrying and with carrying) and three 4-digit numbers -
Word Problems on 4-Digit Numbers |Addition and Subtraction of 4-Digits
Jan 10, 25 02:49 PM
We will solve here some of the word problems on addition and subtraction of 4-digit numbers. We will apply the same method while adding and subtracting the word problems. 1. In a village, there are 25…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.