Area of a Square
In area of a square we will learn how to find the area by counting squares.
To find the area of a region of a closed plane figure, we draw the figure on a centimeter squared paper and then count the number of squares enclosed by the figure.
We know, that square is a rectangle whose length and breadth are equal. In a square all four sides are equal.
Therefore, area of a square = (side × side) square units = (side)2 square units.
In a square the length is equal to breadth.
Hence, area of a square = side × side
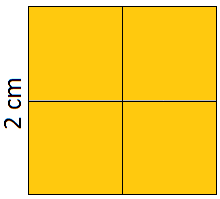
The number of 1 cm squares enclosed = 4
Area = 4 sq cm
4 = 2 × 2
Hence, area = side × side
The unit of sides and the corresponding units of areas as given below:
|
Unit of Side |
Unit of Area |
|
mm |
square mm (sq mm) or mm2 |
|
cm |
square cm (sq cm) or cm2 |
|
m |
square m (sq m) or m2 |
|
km |
square km (sq km) or km2 |
Note: Write finding the area of a given figure, make sure that the sides (length or breadth) are in the same unit of length. If they are given in different units, change them to the same unit.
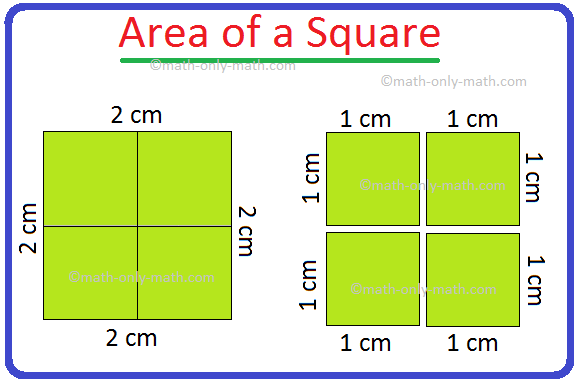
Look at the above figure. You can see that the area of a square having sides 2 cm each is equal to the area of 4 squares of sides 1 cm each = 4 cm2. It can also be expressed as 2 cm × 2 cm = 4 cm2. Area of a square is 2 times of its each side.
Solved examples to find the area of a square when side is given:
1. Find the area of a square of side 8 cm.
Area of a square = length (l) × length (l)
= 8 × 8 sq. cm.
= 64 sq. cm.
2. Find the area of a square of side 11 m.
Area of a square = length × length
= 11 × 11 sq. m.
= 121 sq. m.
3. Find the area of a square of side 49 cm.
Area of a square = length × length
= 49 × 49 sq. cm.
= 2401 sq. cm.
4. Find the area of a square of side 50 m.
Area of a square = length × length
= 50 × 50 sq. m.
= 2500 sq. m.
5. Find the area of a square photo frame whose side is 20 cm.
Area of the photo frame = 20 cm × 20 cm
= 400 sq. cm
6. Find the area of a square with side 9 cm.
Solution:
Area of the square = side x side
= 9 × 9 sq. cm
= 81 sq. cm
Worksheet on Area of a Square:
1. Find the area of the squares with the given side.
(i) 4 cm
(ii) 2.5 cm
(iii) 8 m
(iv) 90 mm
(v) 13.4 km
Answers:
(i) 16 sq. cm
(ii) 6.25 sq. cm
(iii) 64 sq. m
(iv) 8100 sq. m
(v) 179.56 sq. km
2. Find the area of the squares whose side is:
(i) 4 cm
(ii) 20 cm
(iii) 6 m
(iv) 200 m
(v) 12 cm
(vi) 40 cm
Answers:
(i) 16 sq. cm
(ii) 2500 sq. cm
(iii) 36 sq. m
(iv) 40000 sq. m
(v) 144 sq. cm
(vi) 1600 sq. cm
Word Problems on Area of a Square:
3. The area of a badminton court is 140 square m. If the breadth of the court is 7 m, then find its length.
Answer:
20 m
4. The display board of class VII A is in the shape of a square. If the length of its side is 60 cm, then find its area.
Answer:
3600 sq. cm
You might like these
5th Grade Area and Perimeter Worksheet | With Answers | Free Worksheet
In 5th Grade Area and Perimeter Worksheet you will get different types of questions on perimeter of a triangle, perimeter of a square, perimeter of a rectangle, shapes of different kinds with the same perimeter, word problems on perimeter of a rectangle, word problems on
Perimeter and Area of Plane Figures | Definition of Perimeter and Area
A plane figure is made of line segments or arcs of curves in a plane. It is a closed figure if the figure begins and ends at the same point. We are familiar with plane figures like squares, rectangles, triangles and circles. Definition of Perimeter: The perimeter (P) of a
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find the perimeter of the triangles having the following sides.
Worksheet on Area and Perimeter of Rectangles | Word Problems |Answers
Recall the topic and practice the math worksheet on area and perimeter of rectangles. Students can practice the questions on area of rectangles and perimeter of rectangles. 1. Find the area and perimeter of the following rectangles whose dimensions are: (a) length = 17 m
Areas of Irregular Figures | Area of Irregular Shapes | Free Worksheet
Areas of irregular figures can be determined by dividing the figure into squares and rectangles. Some irregular figures are made of rectangular or square regions. The areas of such irregular figures can be determined by calculating the areas of these rectangles and squares.
Worksheet on Area | Test on Area | Home work on Area | Quiz on Area
In worksheet on area we will solve different types of question in area. 1. Find the area of a rectangle of length 24 cm and breadth 13 cm. 2. Find the area of a square of side 40 cm. 3. Find the area of a square of side 21 m.
Word Problems on Area and Perimeter | Free Worksheet with Answers
We will solve different types of word problems on area and perimeter. 1. The perimeter of a rectangular field is 260 m. If its length is 90 m, find its breadth.
Perimeter and Area of Irregular Figures | Solved Example Problems
Here we will get the ideas how to solve the problems on finding the perimeter and area of irregular figures. The figure PQRSTU is a hexagon. PS is a diagonal and QY, RO, TX and UZ are the respective distances of the points Q, R, T and U from PS. If PS = 600 cm, QY = 140 cm
Mental Math on Perimeter and Area | Maths Questions Answers
In mental math on perimeter and area we will solve different type of problems on perimeter of a triangle, perimeter of a square and a rectangle, area of a rectangle, area of a square and word problems on area.
Worksheet on Area of a Square and Rectangle | Area of Squares & Rectan
We will practice the questions given in the worksheet on area of a square and rectangle. We know the amount of surface that a plane figure covers is called its area. 1. Find the area of the square length of whose sides are given below: (i) 15 m (ii) 250 m (iii) 25 cm
Area of a Rectangle | Area of Rectangle = Length × Breadth | Examples
Area of a rectangle is discussed here. We know, that a rectangle has length and breadth. Let us look at the rectangle given below. Each rectangle is made of squares. The side of each square is 1 cm long. The area of each square is 1 square centimeter.
Area | Units to find Area | Conversion Table of Area | Two Dimensional
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed plane figures. In the following figures, the shaded region of each of the
To find Area of a Rectangle when Length and Breadth are of Different Units.
To find Length or Breadth when Area of a Rectangle is given.
To find Cost of Painting or Tilling when Area and Cost per Unit is given.
To find the Number of Bricks or Tiles when Area of Path and Brick is given.
Worksheet on Area of a Square and Rectangle
5th Grade Geometry
5th Grade Math Problems
From Area of a Square to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns
Dec 13, 24 08:43 AM
We see so many patterns around us in our daily life. We know that a pattern is an arrangement of objects, colors, or numbers placed in a certain order. Some patterns neither grow nor reduce but only r… -
Patterns in Math | Missing Number | Counting Numbers | Worksheets
Dec 13, 24 12:31 AM
Finding patterns in math is very important to understand the sequence in the series. We need to find the exact missing number that from the group of numbers. The counting numbers may be counting -
Concept of Pattern | Similar Patterns in Mathematics | Similar Pattern
Dec 12, 24 11:22 PM
Concept of pattern will help us to learn the basic number patterns and table patterns. Animals such as all cows, all lions, all dogs and all other animals have dissimilar features. All mangoes have si… -
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 12, 24 10:31 PM
2nd grade geometry worksheet -
Types of Lines |Straight Lines|Curved Lines|Horizontal Lines| Vertical
Dec 09, 24 10:39 PM
What are the different types of lines? There are two different kinds of lines. (i) Straight line and (ii) Curved line. There are three different types of straight lines. (i) Horizontal lines, (ii) Ver…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.