Perimeter and Area of Irregular Figures
Here we will get the ideas how to solve the problems on finding the perimeter and area of irregular figures.
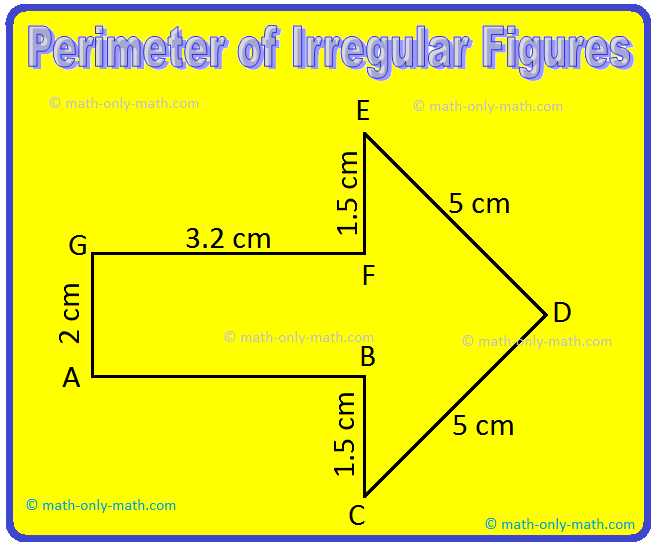
1. Find the perimeter of the given figure.
Solution:
Perimeter = AB + BC + CD + DE + EF + FG + GA
= 3.2 cm + 1.5 cm + 5 cm + 5 cm + 1.5 cm + 3.2 cm + 2 cm
= 21.4 cm
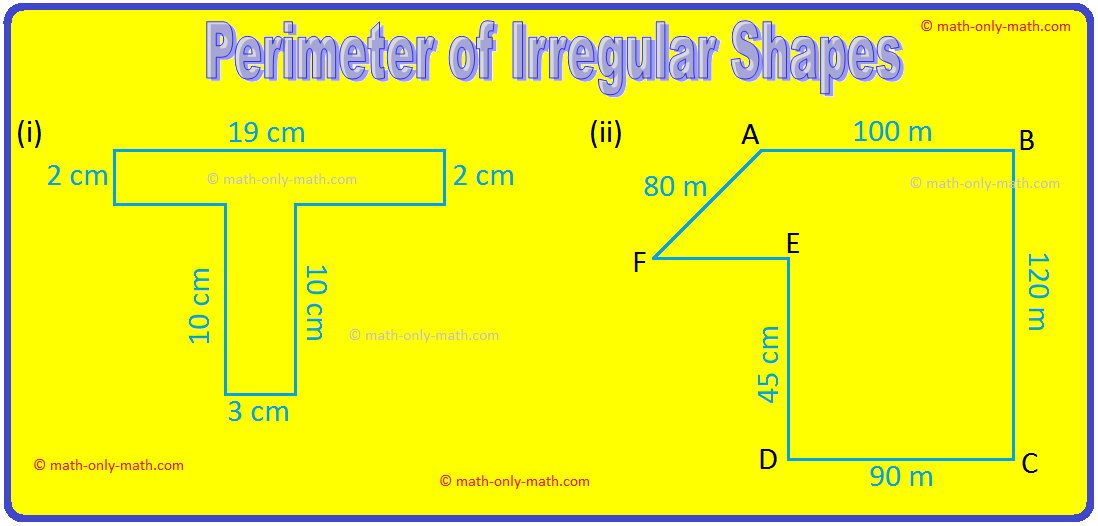
2. Find the perimeter of each of the following figures:
(i) Perimeter of the region = (2 + 19 + 2 + 9 + 10 + 3 + 10 + 7) cm
= 62 cm.
(ii) Perimeter = AB + BC + CD + DE + EF + AF
= (100 + 120 + 90 + 45 + 60 + 80) m
= 495 m .
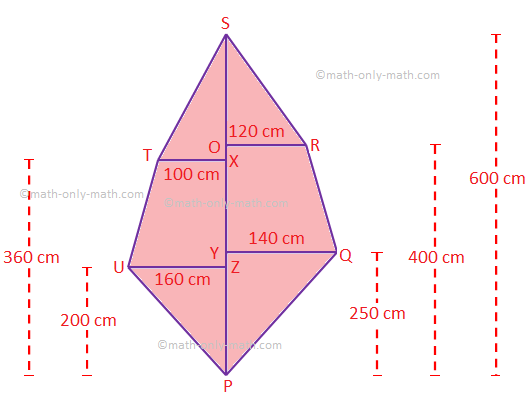
3. The figure PQRSTU is a hexagon.
PS is a diagonal and QY, RO, TX and UZ are the respective distances of the points Q, R, T and U from PS. If PS = 600 cm, QY = 140 cm, RO = 120 cm, TX = 100 cm, UZ = 160 cm, PZ = 200 cm, PY = 250 cm, PX = 360 cm and PO = 400 cm. Find the area of the hexagon PQRSTU.
Solution:
Area of the hexagon PQRSTU = area of ∆PZU + area of
trapezium TUZX + area of ∆TXS + area of ∆PYQ + area of trapezium QROY + area of
∆ROS
= {\(\frac{1}{2}\) × 200 × 160 + \(\frac{1}{2}\) (100 + 160)(360 – 200) + \(\frac{1}{2}\) (600 – 360) × 100 + \(\frac{1}{2}\) × 250 × 140 + \(\frac{1}{2}\) (120 + 140) (400 – 250) + \(\frac{1}{2}\) (600 – 400) × 120} cm\(^{2}\)
= (16000 + 130 × 160 + 120 × 100 + 125 × 140 + 130 × 150 + 100 × 120) cm\(^{2}\)
= (16000 + 20800 + 12000 + 17500 + 19500 + 12000) cm\(^{2}\)
= 97800 cm\(^{2}\)
= 9.78 m\(^{2}\)
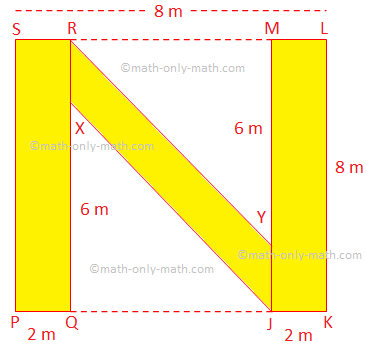
4. In a square lawn of side 8 m, an N-shaped path is made, as shown in the figure. Find the area of the path.
Solution:
Required area = area of the rectangle PQRS + area of the parallelogram XRYJ + area of the rectangle JKLM
= (2 × 8 + PC × BE + 2 × 8) m\(^{2}\)
= (16 + 2 × 4 + 16) cm\(^{2}\)
= 40 m\(^{2}\)
We can solve this problem using another method:
Required area = Area of the square PSLK – Area of the ∆RYM – Area of the ∆XQJ
= [8 × 8 - \(\frac{1}{2}\){8 – (2 + 2)} × 6 - \(\frac{1}{2}\){8 – (2 + 2)} × 6] m\(^{2}\)
= (64 – 12 – 12) m\(^{2}\)
= 40 m\(^{2}\)
You might like these
5th Grade Area and Perimeter Worksheet | With Answers | Free Worksheet
In 5th Grade Area and Perimeter Worksheet you will get different types of questions on perimeter of a triangle, perimeter of a square, perimeter of a rectangle, shapes of different kinds with the same perimeter, word problems on perimeter of a rectangle, word problems on
Perimeter and Area of Plane Figures | Definition of Perimeter and Area
A plane figure is made of line segments or arcs of curves in a plane. It is a closed figure if the figure begins and ends at the same point. We are familiar with plane figures like squares, rectangles, triangles and circles. Definition of Perimeter: The perimeter (P) of a
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find the perimeter of the triangles having the following sides.
Worksheet on Area and Perimeter of Rectangles | Word Problems |Answers
Recall the topic and practice the math worksheet on area and perimeter of rectangles. Students can practice the questions on area of rectangles and perimeter of rectangles. 1. Find the area and perimeter of the following rectangles whose dimensions are: (a) length = 17 m
Areas of Irregular Figures | Area of Irregular Shapes | Free Worksheet
Areas of irregular figures can be determined by dividing the figure into squares and rectangles. Some irregular figures are made of rectangular or square regions. The areas of such irregular figures can be determined by calculating the areas of these rectangles and squares.
From Perimeter and Area of Irregular Figures to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns
Dec 13, 24 08:41 AM
We see so many patterns around us in our daily life. We know that a pattern is an arrangement of objects, colors, or numbers placed in a certain order. Some patterns neither grow nor reduce but only r… -
Patterns in Math | Missing Number | Counting Numbers | Worksheets
Dec 13, 24 12:31 AM
Finding patterns in math is very important to understand the sequence in the series. We need to find the exact missing number that from the group of numbers. The counting numbers may be counting -
Concept of Pattern | Similar Patterns in Mathematics | Similar Pattern
Dec 12, 24 11:22 PM
Concept of pattern will help us to learn the basic number patterns and table patterns. Animals such as all cows, all lions, all dogs and all other animals have dissimilar features. All mangoes have si… -
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 12, 24 10:31 PM
2nd grade geometry worksheet -
Types of Lines |Straight Lines|Curved Lines|Horizontal Lines| Vertical
Dec 09, 24 10:39 PM
What are the different types of lines? There are two different kinds of lines. (i) Straight line and (ii) Curved line. There are three different types of straight lines. (i) Horizontal lines, (ii) Ver…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.