Subscribe to our YouTube channel for the latest videos, updates, and tips.
Transversal Line
What are Transversal Line?
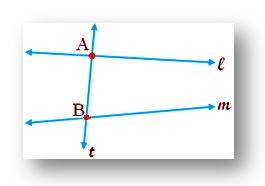
The line which intersects two distinct lines in a plane at two distinct points is called a transversal.
In the below figure, line 't' is transversal to lines l and m, intersecting these two lines at points A and B.
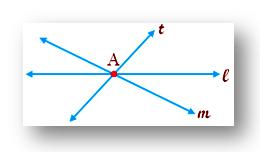
Also, we observe in the below figure, line 't' is not transversal line because it intersects line l and m at one point only.
Angles made by the transversal with two lines:
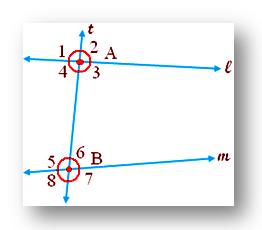
l and m are two lines in a plane. Transversal 't' intersects these two lines at points A and B. Eight angles are formed, i.e., ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7, ∠8. The angles marked have their special names.
Interior angles:
Angles whose arms include AB are called interior angles. In the given figure, ∠3, ∠4, ∠5, ∠6 are interior angles.
Exterior angles:
Angles whose arms do not include AB are called exterior angles. In the given figure ∠1, ∠2, ∠7, ∠8 are exterior angles.
Pair of corresponding angles:
These are pair of angles:
• Which lie on the same side of the transversal.
• If one is an interior angle, the other will be an exterior angle.
• They do not form a linear pair. In the figure, corresponding angles are: (∠2, ∠6); (∠3, ∠7); (∠1, ∠5); (∠4, ∠8)
Pair of alternate angles:
These are pairs of angles:
• Which lie on opposite sides of transversal.
• Both are either exterior angles or both are interior angles.
• They do not form a linear pair. In the given figure, alternate angles are:
(∠4, ∠6); (∠3, ∠5) these are interior alternate angles. In these pair of arms, arm AB is included.
(∠1, ∠7); (∠2, ∠8) these are exterior alternate angles. They do not include arm AB.
Pair of co-interior or conjoined or allied angles:
These are pairs of interior angles which lie on the same side on the transversal. In the given figure, co-interior angles are (∠3, ∠6); (∠4, ∠5)
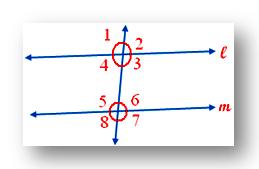
Results when two parallel lines are cut by the transversal:
When parallel lines 'l' and 'in' are cut by the transversal line 't' then
• Pairs of corresponding angles are equal ∠2 = ∠6, ∠3 = ∠7, ∠1 = ∠5, ∠4 = ∠8
• Pairs of alternate angles are equal ∠4 = ∠6, ∠3 =∠5 , ∠ 1 = ∠7, ∠2 = ∠8
• Interior angles on the same side of transversal are supplementary ∠6 = 180°, ∠4 + ∠ 5 = 180°
Converse:
When two lines are cut by a transversal and if
• pairs of corresponding angles are equal
• or pairs of alternate angles are equal
• or interior angles on the same side of transversal are supplementary. Then two lines are said to be parallel to each other.
● Lines and Angles
Fundamental Geometrical Concepts
Some Geometric Terms and Results
Complementary and Supplementary Angles
Parallel and Transversal Lines
7th Grade Math Problems
8th Grade Math Practice
From Transversal Line to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Terms Related to Simple Interest | Simple Interest Formula | Principal
Jun 18, 25 02:57 PM
In terms related to simple interest we will learn all the terms related to simple interest. The terms related to simple interest are Interest, Principal, Amount, Simple Interest, Time or period of tim… -
Introduction to Simple Interest | Definition | Formula | Examples
Jun 18, 25 01:50 AM
In simple interest we will learn and identify about the terms like Principal, Time, Rate, Amount, etc. PRINCIPAL (P): The money you deposit or put in the bank is called the PRINCIPAL. -
5th Grade Profit and Loss Percentage Worksheet | Profit and Loss | Ans
Jun 18, 25 01:33 AM
In 5th grade profit and loss percentage worksheet you will get different types of problems on finding the profit or loss percentage when cost price and selling price are given, finding the selling pri… -
Worksheet on Profit and Loss | Word Problem on Profit and Loss | Math
Jun 18, 25 01:29 AM
In worksheet on profit and loss, we can see below there are some different types of questions which we can practice in our homework. -
Calculating Profit Percent and Loss Percent | Profit and Loss Formulas
Jun 15, 25 04:06 PM
In calculating profit percent and loss percent we will learn about the basic concepts of profit and loss. We will recall facts and formula while calculating profit percent and loss percent. Now we wil
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.