tan x - √3 = 0

We will discuss about the general solution of the equation tan x minus square root of 3 equals 0 (i.e., tan x - √3 = 0) or tan x equals square root of 3 (i.e., tan x = √3).

How to find the general solution of the trigonometric equation tan x = √3 or tan x - √3 = 0?

Solution:

We have,

tan x - √3 = 0

⇒ tan x = √3

⇒ tan x = $\frac{π}{3}$

Again, tan x = √3

⇒ tan x = $\frac{π}{3}$

⇒ tan x = (π + $\frac{π}{3}$)

⇒ tan x = tan $\frac{4π}{3}$

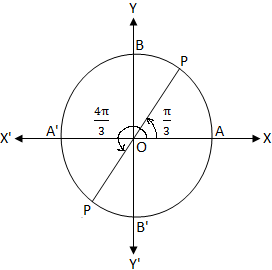
Let O be the centre of a unit circle. We know that in unit circle, the length of the circumference is 2π.

tan x - √3 = 0

If we started from A and moves in anticlockwise direction then at the points A, B, A', B' and A, the arc length travelled are 0, $\frac{π}{2}$, π, $\frac{3π}{2}$, and 2π.

Therefore, from the above unit circle it is clear that the final arm OP of the angle θ lies either in the first or in the final third quadrant.

If the final arm OP lies the first quadrant then,

tan x = √3

⇒ tan x = cos $\frac{π}{3}$

⇒ tan x = ten (2nπ + $\frac{π}{3}$), Where n ∈ I (i.e., n = 0, ± 1, ± 2, ± 3,…….)            

Therefore, x = 2nπ + $\frac{π}{3}$ …………….. (i)

Again, the final arm OP lies in the third quadrant then,

tan x = √3

⇒ tan x = cos $\frac{4π}{3}$

⇒ tan x = ten (2nπ + $\frac{4π}{3}$) , Where n ∈ I (i.e., n = 0, ± 1, ± 2, ± 3,…….)

Therefore, x = 2nπ + $\frac{π}{3}$ …………….. (ii)

Therefore, the general solution of equation tan x - √3 = 0 are the infinite sets of values of x given in (i) and (ii).

Hence general solution of tan x - √3 = 0 is x = nπ + $\frac{π}{3}$, n ∈ I.

● Trigonometric Equations

• General solution of the equation sin x = ½
• General solution of the equation cos x = 1/√2
• General solution of the equation tan x = √3
• General Solution of the Equation sin θ = 0
• General Solution of the Equation cos θ = 0
• General Solution of the Equation tan θ = 0
• General Solution of the Equation sin θ = sin ∝
  
• General Solution of the Equation sin θ = 1
• General Solution of the Equation sin θ = -1
• General Solution of the Equation cos θ = cos ∝
• General Solution of the Equation cos θ = 1
• General Solution of the Equation cos θ = -1
• General Solution of the Equation tan θ = tan ∝
• General Solution of a cos θ + b sin θ = c
• Trigonometric Equation Formula
• Trigonometric Equation using Formula
• General solution of Trigonometric Equation
• Problems on Trigonometric Equation

11 and 12 Grade Math

From tan x - √3 = 0 to HOME PAGE