arccot(x) + arccot(y) = arccot(\(\frac{xy - 1}{y + x}\))
We will learn how to prove the property of the inverse trigonometric function arccot(x) + arccot(y) = arccot(\(\frac{xy - 1}{y + x}\)) (i.e., cot\(^{-1}\) x - cot\(^{-1}\) y = cot\(^{-1}\) (\(\frac{xy - 1}{y + x}\))
Proof:
Let, cot\(^{-1}\) x = α and cot\(^{-1}\) y = β
From cot\(^{-1}\) x = α we get,
x = cot α
and from cot\(^{-1}\) y = β we get,
y = cot β
Now, cot (α + β) = (\(\frac{cot α cot β - 1}{cot β + tan α}\))
cot (α + β) = \(\frac{xy - 1}{y + x}\)
⇒ α + β = cot\(^{-1}\) \(\frac{xy - 1}{y + x}\)
⇒ cot\(^{-1}\) x + cot\(^{-1}\) y = cot\(^{-1}\) \(\frac{xy - 1}{y + x}\)
Therefore, cot\(^{-1}\) x + cot\(^{-1}\) y = cot\(^{-1}\) \(\frac{xy - 1}{y + x}\)
● Inverse Trigonometric Functions
- General and Principal Values of sin\(^{-1}\) x
- General and Principal Values of cos\(^{-1}\) x
- General and Principal Values of tan\(^{-1}\) x
- General and Principal Values of csc\(^{-1}\) x
- General and Principal Values of sec\(^{-1}\) x
- General and Principal Values of cot\(^{-1}\) x
- Principal Values of Inverse Trigonometric Functions
- General Values of Inverse Trigonometric Functions
- arcsin(x) + arccos(x) = \(\frac{π}{2}\)
- arctan(x) + arccot(x) = \(\frac{π}{2}\)
- arctan(x) + arctan(y) = arctan(\(\frac{x + y}{1 - xy}\))
- arctan(x) - arctan(y) = arctan(\(\frac{x - y}{1 + xy}\))
- arctan(x) + arctan(y) + arctan(z)= arctan\(\frac{x + y + z – xyz}{1 – xy – yz – zx}\)
- arccot(x) + arccot(y) = arccot(\(\frac{xy - 1}{y + x}\))
- arccot(x) - arccot(y) = arccot(\(\frac{xy + 1}{y - x}\))
- arcsin(x) + arcsin(y) = arcsin(x \(\sqrt{1 - y^{2}}\) + y\(\sqrt{1 - x^{2}}\))
- arcsin (x) - arcsin(y) = arcsin (x \(\sqrt{1 - y^{2}}\) - y\(\sqrt{1 - x^{2}}\))
- arccos (x) + arccos(y) = arccos(xy - \(\sqrt{1 - x^{2}}\)\(\sqrt{1 - y^{2}}\))
- arccos(x) - arccos(y) = arccos(xy + \(\sqrt{1 - x^{2}}\)\(\sqrt{1 - y^{2}}\))
- 2 arcsin(x) = arcsin(2x\(\sqrt{1 - x^{2}}\))
- 2 arccos(x) = arccos(2x\(^{2}\) - 1)
- 2 arctan(x) = arctan(\(\frac{2x}{1 - x^{2}}\)) = arcsin(\(\frac{2x}{1 + x^{2}}\)) = arccos(\(\frac{1 - x^{2}}{1 + x^{2}}\))
- 3 arcsin(x) = arcsin(3x - 4x\(^{3}\))
- 3 arccos(x) = arccos(4x\(^{3}\) - 3x)
- 3 arctan(x) = arctan(\(\frac{3x - x^{3}}{1 - 3 x^{2}}\))
- Inverse Trigonometric Function Formula
- Principal Values of Inverse Trigonometric Functions
- Problems on Inverse Trigonometric Function
11 and 12 Grade Math
From arccot(x) + arccot(y) to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
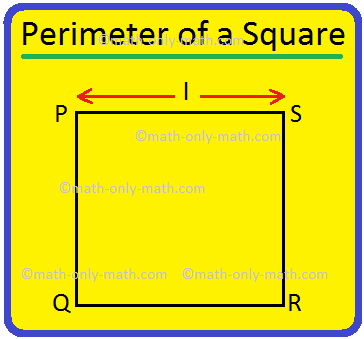
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete… -
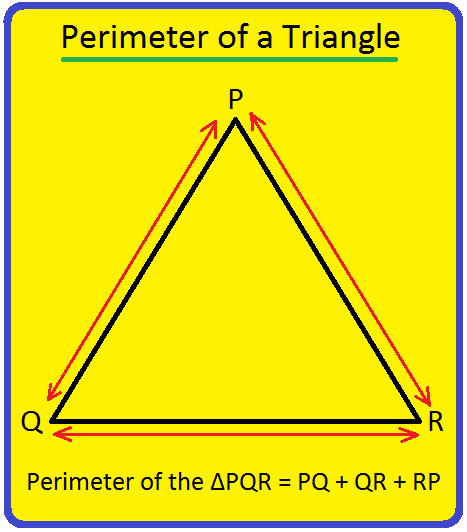
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
Apr 25, 24 05:13 PM
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of length… -
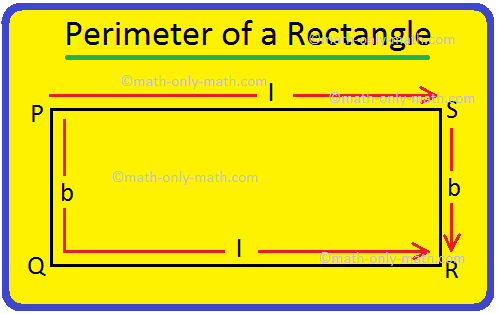
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
Apr 25, 24 03:45 PM
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opp… -
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Apr 24, 24 03:46 PM
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit nu… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 24, 24 03:45 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi…