Linear Symmetry
What is a linear symmetry?
It is type of symmetry in which a line is drawn from the middle of the figure.
The two parts of the figure coincide, then each part is called the mirror image of the other i.e., the part of the figure on one side of the dotted line falls exactly over the other part which lies on the side. Such a figure is called a symmetrical figure.
The line which divides the figure into two equal parts is called the line of symmetry or axis of symmetry.
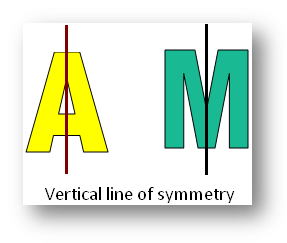
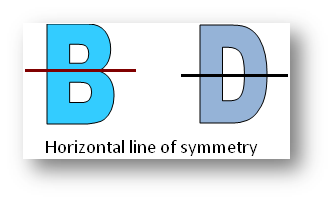
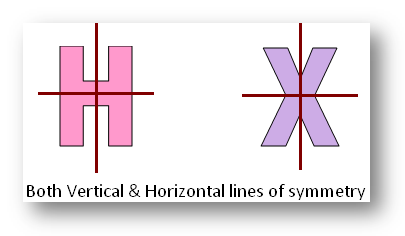
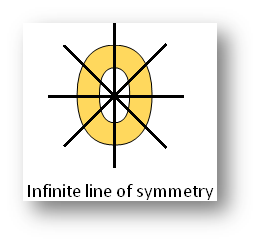
Shapes or figures may have horizontal, vertical, both horizontal and vertical, infinite and no line of symmetry.
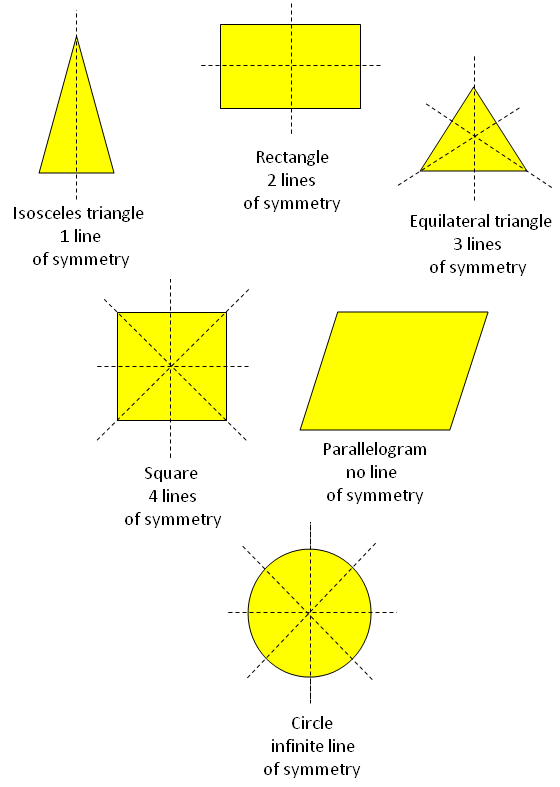
Examples of the different types of pictures of horizontal line of symmetry, vertical line of symmetry, both horizontal and vertical lines of symmetry, infinite lines of symmetry and no line of symmetry.
Examples of the shapes or figures may have 1, 2, 3, 4, 0 and so on or infinite lines of symmetry.
Isosceles triangle has two sides equal and two angles equal showing one line of symmetry.
Rectangle has opposite sides equal and all the angles 90° showing two lines of symmetry.
Equilateral triangle have all three sides equal and all three angles equal showing three lines of symmetry.
Square have all four sides equal and all angles 90° showing four lines of symmetry.
Parallelogram has opposite sides equal and parallel sides equal showing no line of symmetry.
Circle showing infinite lines of symmetry.
● Related Concepts
● Order of Rotational Symmetry
● Reflection of a Point in x-axis
● Reflection of a Point in y-axis
● Reflection of a point in origin
● Rotation
● 90 Degree Clockwise Rotation
● 90 Degree Anticlockwise Rotation
7th Grade Math Problems
8th Grade Math Practice
From Linear Symmetry to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
|
|
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.