Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Point Symmetry
Point symmetry exists when the figure is drawn around a single point.
This point is called the centre of the figure or the centre of the symmetry. In the adjoining figure, we observe that corresponding to point X on the figure, there exists a point X’ on the other side of the centre which is directly opposite to X and lies on the figure. We say that the figure is symmetry about the centre.
Note:
When we rotate a figure about 180° and it regains its originals shape, then we say that point symmetry exists in the figure.
Examples of the figures exhibiting point symmetry:
● All letters of the English alphabet.
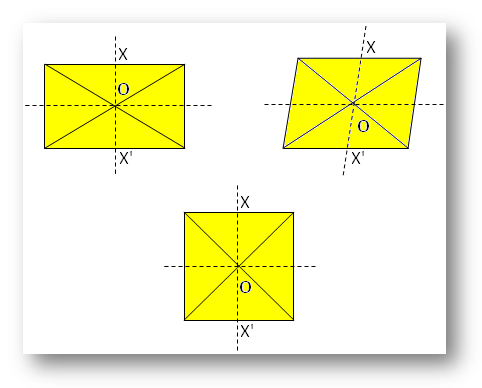
● Different geometrical figures.
Note:
Here, O is the centre of symmetry.
With respect of X there exists X’, such that X’ is directly opposite to X on the other side of O.
What are the conditions that a shape or a figure satisfies for point symmetry?
The conditions that a shape or a figure satisfies for point symmetry i.e. every part should have a matching part
• the distance should be equal from the central point
• but should be in the opposite direction.
● Related Concepts
● Order of Rotational Symmetry
● Reflection of a Point in x-axis
● Reflection of a Point in y-axis
● Reflection of a point in origin
● Rotation
● 90 Degree Clockwise Rotation
● 90 Degree Anticlockwise Rotation
7th Grade Math Problems
8th Grade Math Practice
From Point Symmetry to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

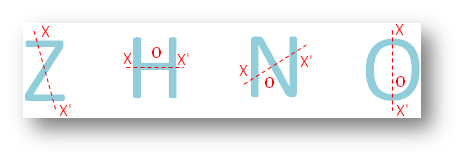


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.