Rotational Symmetry

What is rotational symmetry?

When the figure is turned about a fixed point; it is called rotation.

The shapes and objects that look the same after a certain amount of rotation are said to have rotational symmetry. Some shapes look the same after half a turn. If we turn English alphabet S around a centre point by 180° we get the alphabet S in the same position. The angle of turning during a rotation is called the angle of rotation. A complete turn means 360°, so a half turn means 180° and a quarter turn means 90°.

This rotation can be: (a) clockwise (b) anticlockwise

The fixed about which the figure is rotated is called centre of rotation.

The angle of turning during rotation is called the angle of rotation.

A quarter turn means a rotation of 90°

A half turn means a rotation of 180°

A full turn means a rotation of 360°

A figure is said to have rotational symmetry if it onto more than once during a complete rotation, i.e., 360°

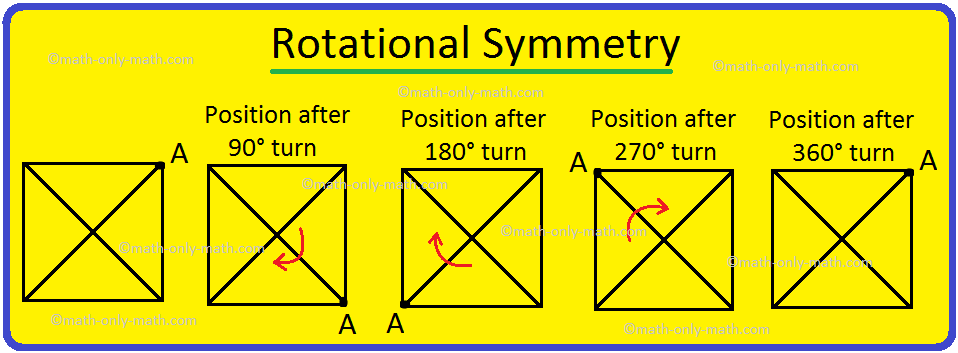
Take a square piece and draw lines, as shown in the figure. Place a pin in the centre where the lines meet. Now, rotate this square by 90° about its centre. The square looks exactly the same. In a full turn 360° there are 4 positions when the square looks exactly the same.

Thus, a square has a rotational symmetry of order 4 about its centre of rotation. Hence, the angle of rotation is 90°.

Order of rotational symmetry = $\frac{360}{\textrm{Angle of Rotation}}$

A figure has a rotational symmetry of order 1, if it can come to its original position after full rotation or 360°.

● Related Concepts

● Linear Symmetry

● Lines of Symmetry

● Point Symmetry

● Order of Rotational Symmetry

● Types of Symmetry

● Reflection

● Reflection of a Point in x-axis

● Reflection of a Point in y-axis

● Reflection of a point in origin

● Rotation

● 90 Degree Clockwise Rotation

● 90 Degree Anticlockwise Rotation

● 180 Degree Rotation

7th Grade Math Problems

8th Grade Math Practice

From Rotational Symmetry to HOME PAGE