Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Absolute Value of an Integer
Absolute value of an integer is its numerical value without taking the sign into consideration.
The absolute values of -9 = 9; the absolute value of 5 = 5 and so on.
The symbol used to denote the absolute value is, two vertical lines (| |), one on either side of an integer.
Therefore, if 'a' represents an integer, its absolute value is represented by |a| and is always non-negative.
Note:
(i) |a| = a; when 'a' is positive or zero.
(ii) |a| = -a; when 'a' is negative.
Definition of Absolute Value of an Integer:
The numerical value of an integer regardless of its sign is known as its absolute value.
The two vertical bars | | represent the absolute value.
If x represents an integer, then
| x | = x if x is +ve or zero
| -x | = x if x is -ve.
The absolute value of 5, written as |5|, is 5 and the absolute value of -5, written as| -5|, is 5.
The absolute value of 15, written as | 15 |, is 15 and the absolute value of -15, written as | -15 |, is 15.
The absolute value of 0, written as | 0 |, is 0.
Find the absolute value of the following:
(i) -76
(ii) +50
(iii) -100
Solution:
(i) -76 = |76|
(ii) +50 = |50|
(iii) -100 = |100|
Examples on absolute value of an integer:
(i) Absolute value of - 7 is written as |- 7| = 7 [here mod of - 7 = 7]
(ii) Absolute value of + 2 is written as |+ 2| = 2 [here mod of + 2 = 2]
(iii) Absolute value of - 15 is written as |- 15| = 15 [here mod of - 15 = 15]
(iv) Absolute value of + 17 is written as |+ 17| = 17 [here mod of + 17 = 17]
On a number line the number indicates the distance from 0 and the sign before the number tells us whether the distance is to the right or left of 0. For example +5 is 5 units away to the right of 0 where as -5 is 5 units away to the left of 0 on the number line. The numerical value of the unit regardless of the sign is called absolute value of an integer. The absolute value of an integer is always positive. Thus, the absolute value of 5 and -5 is 5. It is written as |5|
So, |5| = 5 and |-5| = 5
Find the mod of:
(i) |14 - 6| = |8| = 8
(ii) - |- 10| = - 10
(iii) 15 - |- 6| = 15 - 6 = 9
(iv) 7 + |- 7| = 7 + 7 = 14
Note: (i) A positive number with a sign in front of its numerical value means increase or gain.
(ii) A negative number with a sign in front of its numerical value means decrease or loss.
Different Types of Solved Examples on Absolute Value of an Integer:
1. Write the opposites of the following statements:
(i) 28 m to the right
(ii) running 75 km towards East
(iii) loss of $ 250
(iv) 780 m above sea level
(v) increase in population
Solution:
(i) 28 m to the left
(ii) running 75 km towards West
(iii) gain of $ 250
(iv) 780 m below sea level
(v) decrease in population
2. Represent the following numbers as integers with appropriate signs.
(i) 7°C above normal temperature
(ii) A deposit of $5690
(iii) 23°C below 0°C
Solution:
(i) +7°C
(ii) +$5690
(iii) -23°C
3. Compare -2 and -6 using number line
Solution:
Since -2 is to the right of -6, therefore -2 > -6 or -6 < -2.
4. Find the absolute value of each of the following:
(i) -12
(ii) 30
(iii) 0
Solution:
(i) The absolute value of -12 = | -12 | = 12
(ii) The absolute value of 30 = | 30 | = 30
(ii) The absolute value of 0 = | 0 | = 0
[Since integer 0 is neither positive nor negative, the absolute value of zero is zero i.e., | 0 | = 0.
5. Find the value of 24 + | -14 |.
Solution:
24 + | -14 |.
= 24 + 14, since | -14 | = 14.
6. Write all the integers between
(i) -1 and 3
(ii) -3 and 4
Solution:
(i) The integers between -1 and 3 are 0, 1, 2.
(ii) The integers between -3 and 4 are -2, -1, 0, 1, 2, 3.
7. Which of the following pairs of integers is greater?
(i) 6, -6
(ii) 0, -9
(iii) 0, 8
(iv) -8, -3
(v) 4, -9
Solution:
(i) 6 > -6; since, every positive integer is greater than every negative integer.
(ii) 0 > -9; since, 0 is greater than every negative integer.
(iii) 0 < 8; Since, 0 is less than every positive integer.
(iv) -8 < -3; Since, If x = 8 and b = 3 then x > y, therefore, -x < -y.
(v) 4 > -9; Since, every positive integer is greater than every negative integer.
8. Write the absolute value of each of the following:
(i) -98
(ii) 250
(iii) -2953
Solution:
(i) Absolute value of - 98 = |- 98| = 98
(ii) Absolute value of 250 = |250| = 250
(iii) Absolute value of - 2953 = |- 2953| = 2953
9. Write the integers given below in:
(i) increasing order
(ii) decreasing order.
34, 0, -7, -1, 8, -9, -50
Solution:
(i) The integers in increasing order are:
-50, -9, -7, -1, 0, 8, 34
(ii) The integers in decreasing order are:
34, 8, 0, -1, -7, -9, -50
10. Find the value of each of the following:
(i) |7| + |- 5|
(ii) |- 7| - |0|
Solution:
(i) |7| + |- 5| = 7 + 5 = 12
(ii) |- 7| - |0| = 7 + 0 = 7
1. What is the absolute value of an integer?
1. What is the absolute value of an integer?
Answer:
The absolute value of an integer is the numerical value of the integer regardless of its sign.
Hence, the absolute value of any integer is always positive.
We use the symbol ||, called modulus, to denote the absolute value.
The absolute value of -5 is expressed as |- 5| = 5 and |+5| = 5
If the absolute value of an integer is 8, integer can be +8 or -8.
● Numbers - Integers
Properties of Multiplication of Integers
Examples on Multiplication of Integers
Properties of Division of Integers
Examples on Division of Integers
Examples on Fundamental Operations
● Numbers - Worksheets
Worksheet on Multiplication of Integers
Worksheet on Division of Integers
Worksheet on Fundamental Operation
7th Grade Math Problems
From Absolute Value of an Integer to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.


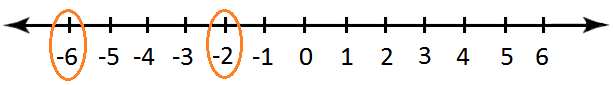


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.