Comparison of Integers
We know that on a number line the number on the right is always greater than the number on the left. Same applies for integers also. -1 > -2, -2 > -3 and so on.
From the above number line we can say that 0 separates the positive and negative integers. 0 is on the left of all the positive integers. So, 0 is less than every positive integer. 0 is on the right of all the negative integers. So, 0 is greater than every negative integer. All the positive integers are greater than negative integers.
Comparison of integers: When we represent integers on the number line, we observe that the value of the number increases as we move towards right and decreases as we move towards left.
1 < 2 < 3 …..
-1 > -2 > ……
The whole numbers are on the right side of the 0 and in the left side of the 0 there are negative numbers.
Note:
(i) Zero is less than every positive integer, and greater than every negative integer. Zero is neither positive nor negative.
For example, 0 < 1, 0 < 10, etc.
Also 0 > -1, 0 > -5, etc.
(ii) Every positive integer is greater than every negative integer.
For example, 2 > -2, 2 > -1, 1 > -1 etc.
(iii) There is no greatest or smallest integer.
(iv) The smallest positive integer is 1 and the greatest negative integer is -1.
Solved Examples on Comparison of Integers:
1. Which is greater +1 or -6?
Solution:
Since +1 lies to the right of 0 on the number line. +1 is greater than -6.
2. Which is greater -27 or -34?
Solution:
-34 is 34 units away to the left of 0. -27 is 27 units away to the left of 0. So, -27 is to the right of -34. -27 > -34.
3. Arrange +27, -32, +16 and -12 in ascending order.
Solution:
Let us mark the integers on the number line.
Thus, the integers in ascending order are -33, -15, +18, +29
● Numbers - Integers
Properties of Multiplication of Integers
Examples on Multiplication of Integers
Properties of Division of Integers
Examples on Division of Integers
Examples on Fundamental Operations
● Numbers - Worksheets
Worksheet on Multiplication of Integers
Worksheet on Division of Integers
Worksheet on Fundamental Operation
7th Grade Math Problems
From Comparison of Integers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheets on Comparison of Numbers | Find the Greatest Number
Oct 10, 24 05:15 PM
In worksheets on comparison of numbers students can practice the questions for fourth grade to compare numbers. This worksheet contains questions on numbers like to find the greatest number, arranging… -
Counting Before, After and Between Numbers up to 10 | Number Counting
Oct 10, 24 10:06 AM
Counting before, after and between numbers up to 10 improves the child’s counting skills. -
Expanded Form of a Number | Writing Numbers in Expanded Form | Values
Oct 10, 24 03:19 AM
We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its… -
Place Value | Place, Place Value and Face Value | Grouping the Digits
Oct 09, 24 05:16 PM
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know th… -
3-digit Numbers on an Abacus | Learning Three Digit Numbers | Math
Oct 08, 24 10:53 AM
We already know about hundreds, tens and ones. Now let us learn how to represent 3-digit numbers on an abacus. We know, an abacus is a tool or a toy for counting. An abacus which has three rods.
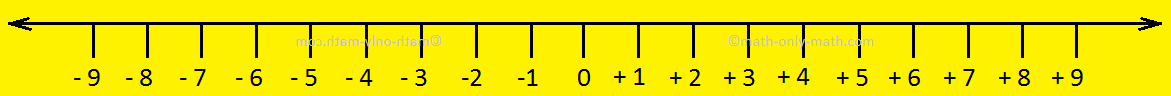
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.