Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Integers
In integers we know that the numbers are
........... -6, -5, -4, - 3,- 2,- 1, 0, 1, 2, 3, 4, 5, 6, ...........
The numbers 1, 2, 3, 4, 5, 6, 7, 8, ........, i.e. natural numbers, are called positive integers
and the numbers - 1,- 2, - 3, - 4, - 5, - 6, -7, -8, ........, are called negative integers.
The number 0 is simply an integer. It is neither positive nor negative.
We know about the addition and subtraction of integers. In seventh grade math under integers we will learn about multiplication and division of integers. We will also learn about various properties of these operations on integers.
In integers we will discuss on this in details and solve various types of examples on integers.
● The numbers ........, -6, -5, -4, -3,-1, 0, 1, 2, 3, 4, 5, 6, ........ etc. are integers.
● 1, 2, 3, 4, 5, 6, 7, ........ are positive integers and -1, -2, -3, -4, -5, -6, -7, ........ are negative integers.
● 0 is an integer which is neither positive nor negative.
● On an integer number line, all numbers to the right of 0 are positive integers and all numbers to the left of 0 are negative integers.
● 0 is less than every positive integer and greater than every negative integer.
● Every positive integer is greater than every negative integer.
● Two integers that are at the same distance from 0, but on opposite sides of it are called opposite numbers.
● The greater the number, the lesser is its opposite.
● The sum of an integer and its opposite is zero.
● The absolute value of an integer is the numerical value of the integer without regard to its sign. The absolute value of an integer x is denoted by |x| and is given by
● The sum of two integers of the same sign is an integer of the same sign whose absolute value is equal to the sum of the absolute values of the given integers.
● The sum of two integers of opposite signs is an integer whose absolute value is the difference of the absolute values of addend and whose sign is the sign of the addend having greater absolute value.
● To subtract an integer y from another integer x, we change the sign of y and add it to x.
Thus, x - y = x + (-y)
● All properties of operations on whole numbers are satisfied by these operations on integers.
● If m and n are two integers, then (m - n) is also an integer.
● -m and m are negative or additive inverses of each other.
● To find the product of two integers, we multiply their absolute values and give the result a plus sign if both the numbers have the same sign or a minus sign otherwise.
● To find the quotient of one integer divided by another non-zero integer, we divide their absolute values and give the result a plus sign if both the numbers have the same sign or a minus sign otherwise.
● All the properties applicable to whole numbers are applicable to integers in addition; the subtraction operation has the closure property.
● Any integer when multiplied or divided by 1 gives itself and when multiplied or divided by - 1 gives its opposite.
● When expression has different types of operations, some operations have to be performed before the others. That is, each operation has its own precedence. The order in which operations are performed is division, multiplication, addition and finally subtraction (DMAS) .
● Brackets are used in an expression when we want a set of operations to be performed before the others.
● While simplifying an expression containing brackets, the operations within the innermost set of brackets are performed first and then those brackets are removed followed by the ones immediately after them till all the brackets are removed.
● While simplifying arithmetic expressions involving various parentheses or brackets and operations, we use as PEMDAS rule or BODMAS rule. Both are same some follow PEMDAS rule or some follow BODMAS rule.
● PEMDAS stands for Parentheses, Exponents, Multiplication, Division, Addition, Subtraction.
● BODMAS stands for Brackets, Order, Division, Multiply, Addition, Subtraction.
● Numbers - Integers
Properties of Multiplication of Integers
Examples on Multiplication of Integers
Properties of Division of Integers
Examples on Division of Integers
Examples on Fundamental Operations
● Numbers - Worksheets
Worksheet on Multiplication of Integers
Worksheet on Division of Integers
Worksheet on Fundamental Operation
7th Grade Math Problems
From Integers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
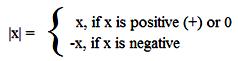


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.