Sample 3

In sample 3 we will find 10 sample questions for math employment test.

(a) √6 + √2

(b) √6 - √2

(c) √6 – 2

(d) 2 - √6

(e) None

2. \((\frac{\sqrt{5} + \sqrt{3}}{\sqrt{5} - \sqrt{3}})^{2}\) is equal to:

(a) 62

(b) 66 

(c) 64

(d) 68

(e) 65

3. The greatest (√19 – √17), (√13 – √11), (√7 – √5) and (√5 – √3) is:

(a) (√19 – √17)

(b) (√13 – √11)

(c) (√7 – √5)

(d) (√5 – √3)

(e) None



4. Arrange the following in descending order:

∛4, √2, √(6&3) , ∜5

(a) √2 > √(6&3) > ∛4 > ∜5

(b) ∜5 > ∛4 > √(6&3) > √2

(c) ∜5 > ∛4 > √2 > √(6&3)

(d) √(6&3) > ∜5 > ∛4 √2

(e) None



5. If x = \(\frac{\sqrt{3} + 1}{\sqrt{3} - 1}\) and y = \(\frac{\sqrt{3} + 1}{\sqrt{3} - 1}\), then value of x² + y²

(a) 13

(b) 14

(c) 15

(d) 10

(e) 8

6. \(\frac{√1296}{?}\) = \(\frac{?}{2.25}\)

(a) 6

(b) 8

(c) 7

(d) 9

(e) 12



7. √(.00059049) =?

(a) .243 

(b) .0243

(c) .00243

(d) .000243

(e) None



8. What is 25% of 25% equal to:

(a) 6.25

(b) .625 

(c) 0.625

(d) .00625

(e) None



9. If 8% of x = 4% of y, then 20% of x is:

(a) 10 % of y 

(b) 16 % of y 

(c) 80 % of y

(d) 15 % of y 

(e) None



10. 75% of a number when added to 75 is equal to the number. The number is:

(a) 150 

(b) 200 

(c) 225

(d) 300

(e) 320 

Answers of Sample 3

After solving the sample3 please go to sample 4

In sample 3 if you have any doubts in solving these 10 questions you can fill-up the Comments box below, so that we can help you.

● Sample 1           Answers of Sample 1

● Sample 2           Answers of Sample 2

● Sample 3           Answers of Sample 3

● Sample 4           Answers of Sample 4

● Sample 5           Answers of Sample 5

● Sample 6           Answers of Sample 6

● Sample 7           Answers of Sample 7

Math Employment Test Samples

From Sample 3 to HOME PAGE

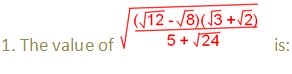
New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit