Reflection of a Point in Origin

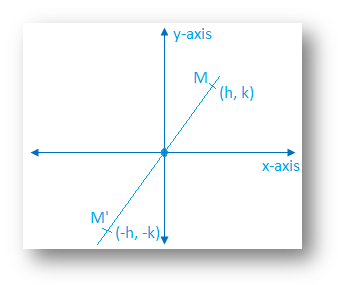
How to find the co-ordinates of the reflection of a point in origin?

To find the co-ordinates in the adjoining figure, origin represents the plane mirror. M is the any point in the first whose co-ordinates are (h, k). When point M is reflected in the origin, the image M’ is formed in the third quadrant whose co-ordinates are (-h, -k).

Thus, we conclude that when a point is reflected in origin, both x-c-ordinate and y-co-ordinate become negative. Thus, the image of M (h, k) is M’ (-h, -k).

Rules to find the reflection of a point in the origin:

(i) Change the sign of abscissa i.e., x-coordinate.

(ii) Change the sign of ordinate i.e., y-coordinate.

For example:

1. The reflection of the point A (5, 7) in the origin is the point A' (-5, -7).

2. The reflection of the point B (-5, 7) in the origin is the point B' (5, -7).

3. The reflection of the point C (-5, -7) in the origin is the point C' (5, 7).

4. The reflection of the point D (5, -7) in the origin is the point D' (-5, 7).

5. The reflection of the point E (5, 0) in the origin is the point E' (-5, 0).

6. The reflection of the point F (0, 7) in the origin is the point F' (0, -7).

7. The reflection of the point G (-5, 0) in the origin is the point G' (5, 0).

8. The reflection of the point H (0, -7) in the origin is the point H' (0, 7).

Worked-out examples to find the co-ordinates of the reflection of a point in origin:

1. What is the reflection of the following in origin?

(i) P (1, 4)

(ii) Q (-3, -7)

(iii) R (-5, 8)

(iv) S (6, -2)

Solution:

(i) The image of P (1, 4) is P’ (-1, -4).

(ii) The image of Q (-3, -7) is Q’ (3, 7).

(iii) The image of R (-5, 8) is R’ (5, -8).

(iv) The image of S (6, -2) is S’ (-6, 2).

Note:

Thus, we conclude that the origin acts as a plane mirror. M is the point whose co-ordinates are (h, k).

The image of M, i.e., M’ lies in the third quadrant and the co-ordinates of M’ are (h, -k).

● Related Concepts

● Lines of Symmetry

● Point Symmetry

● Rotational Symmetry

● Order of Rotational Symmetry

● Types of Symmetry

● Reflection

● Reflection of a Point in x-axis

● Reflection of a Point in y-axis

● Rotation

● 90 Degree Clockwise Rotation

● 90 Degree Anticlockwise Rotation

● 180 Degree Rotation

7th Grade Math Problems

8th Grade Math Practice

From Reflection of a Point in Origin to HOME PAGE