Properties of Triangle

We will discuss here about some of the properties of triangle.

I. Angle Sum Property of a Triangle:

Relation between the measures of three angles of a triangle.

The sum of three angles of every triangle is 180°.

In ∆ABC, ∠A + ∠B + ∠C = 180°,

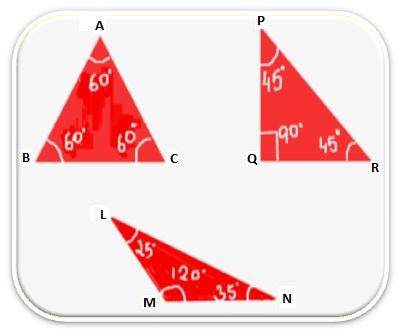
Draw three triangles on your not book. Name them as ∆PQR, ∆ABC and ∆LMN. With the help of protector measure all the angles the angles and find them: In ∆ABC ∠ABC + ∠BCA + ∠CAB = 180° In ∆PQR ∠PQR + ∠QRP + ∠RPQ = 180° In ∆LMN ∠LMN + ∠MNL + ∠NLM = 180°

Here, we observe that in each case, the sum of the measures of three angles of a triangle is 180°.

In the given figure, ∠A = 60°, ∠B = 90° and ∠C = 30°.

We see ∠A + ∠B + ∠C = 60° + 90° + 30° = 180°.

Hence, the sum of the three angles of a triangle is equals to 180°.

Note: If two angles of a triangle are given, we can easily find out its third angle.

Solved Examples on Angle Sum Property of a Triangle:

1. In a right triangle, if one angle is 50°, find its third angle.

Solution:

∆ PQR is a right triangle, that is, one angle is right angle.

Given, ∠PQR = 90°

         ∠QPR = 50°

Therefore, ∠QRP = 180° - (∠Q + ∠ P)

= 180° - (90° + 50°)

= 180° - 140°

∠R = 40°

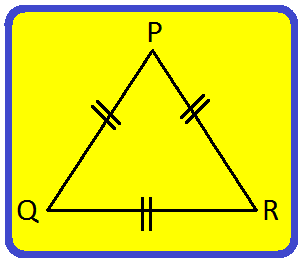
2. PQR is an equilateral triangle. Find the measure of its each angle.

Solution:

PQR is an equilateral triangle. ∠P = ∠Q = ∠R According to the angle sum property of a triangle, we get     ∠P + ∠Q + ∠R = 180° ⟹ ∠P + ∠P + ∠P = 180°; [Since, ∠P = ∠Q = ∠R] ⟹ 3 ∠P = 180° ⟹ ∠P = $\frac{180°}{3}$ ⟹ ∠P = 60° Thus, ∠P= ∠Q= ∠R = 60°

Therefore, each angle of an equilateral triangle is 60°.

3. Two angles of a triangle are 83° and 36°. Find the third angle.

Solution:

The sum of two given angles of the triangle = 83° + 36° = 119°

The sum of all the three angles of the triangle = 180°

So, the third angle = 180° - the sum of two angles

                            = 180° - 119°

                            = 61°

II. Triangle Inequality Property:

Triangle inequality property is the relation between lengths of the side of a triangle.

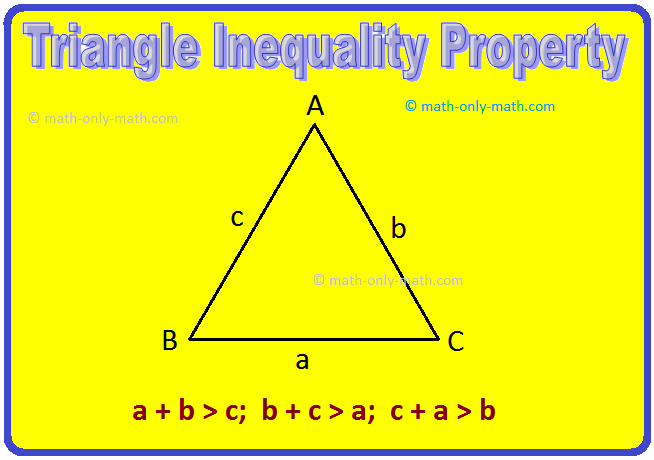
∆ABC has three sides namely AB, BC and CA.

For a shorter notation, the length of the side opposite to the vertex A is written as 'a'

         i.e., a = BC

Similarly, b = CA and c = AB

If we measure the lengths of a, b and c, we find the following relation:

a + b > c

b + c > a

c + a > b

Now, we have the following:

The sum of any two sides in a triangle is greater than the third side.

Solved Examples on Triangle Inequality Property:

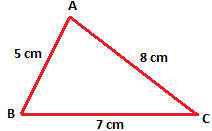
1. Draw a ∆ABC. Measure the length of its three sides.

Let the lengths of the three sides be AB = 5 cm, BC = 7 cm, AC = 8 cm.

Now add the lengths of any two sides compare this sum with the lengths of the third side.

(i) AB + BC = 5 cm + 7 cm = 12 cm

Since 12 cm > 8 cm

Therefore, (AB + BC) > AC

(ii) BC + CA = 7 cm + 8 cm = 15 cm

Since 15 cm > 5 cm

Therefore, (BC + CA) > AB

(iii) CA + AB = 8 cm + 5 cm = 13 cm

Since 13 cm > 7 cm

Therefore, (CA + AB) > BC

In the below figure we can see in each case, if we add up any two sides of the ∆, the sum is more than its third side.

Thus, we conclude that the sum of the length of any two sides of a triangle is greater than the length of the third side.

Solved Examples on Triangle Inequality Property:

1. Is it possible to have a triangle whose sides are 5 cm, 6 cm and 4 cm?

Solution:

The lengths of the sides are 5 cm, 6 cm, 4 cm,

(a) 5 cm + 6 cm > 4 cm.

(b) 6 cm + 4 cm > 5 cm.

(c) 5 cm + 4 cm > 6 cm.

Hence, a triangle with these sides is possible.

2. Which of the following can be the possible lengths (in cm) of a triangle?

(i) 3, 5, 3

(ii) 4, 3, 8

Solution:

(i) Since 3 + 5 (i.e., 8) > 3, 5 + 3 (i.e., 8) > 3 and 3 + 3 (i.e., 6) > 5, therefore 3, 5, 3 (in cm) can be the lengths of the sides of a triangle.

(ii) Since 4 + 3 (i.e., 7) < 8, therefore 4, 3, 8 (in cm) cannot be the lengths of the sides of a triangle.

3. The lengths of three line segments AB, BC and AC are as follows

(i) 3 cm, 5 cm and 6 cm

(ii) 4 cm, 4 cm, 9 cm.

(iii) 2 cm, 4 cm, 8-cm

(iv) 5 cm, 2 cm, 8 cm

In which of the above cases, you can construct a A ABC and in which you cannot and why?

Solution:

(i) The three sides are AB = 3 cm, BC = 5 cm and AC = 6 cm.

Now we see,

                AB + BC > AC as 3 cm + 5 cm > 6 cm

                AB + AC > BC as 3 cm + 6 cm > 5 cm

                BC + AC > AB as 5 cm + 6 cm > 3 cm

So, we can construct the triangle ∆ ABC

(ii) AB = 4 cm, BC = 4 cm, AC = 9 cm

Here, we see, AB + BC < AC

i.e., 4 cm + 4 cm = 8 cm < 9 cm

So, the construction of triangle ABC is not possible.

(iii) AB = 2 cm, BC = 4 cm and AC = 8cm

Here, we see, AB + BC < AC

ie, 2 cm + 4 cm = 6 cm < 8 cm

So, the construction of ∆ ABC is not possible.

(iv) AB = 5 cm, BC = 2 cm, AC = 8 cm

Here, we see, AB + BC < AC

i.e., 5 cm + 2 cm = 7cm < 8 cm

So, the construction of triangle ABC is not possible.

III. Properties of Exterior Angles and Interior Opposite Angles of a Triangle:

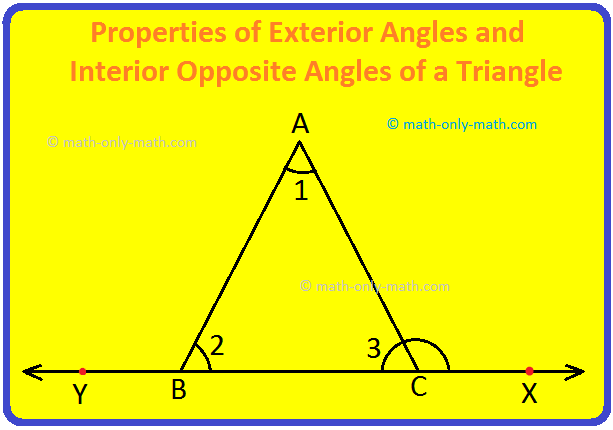
Consider a triangle ABC. Produce its side BC to X.

∠ACX is called an exterior angle of ∆ABC at C.

Similarly, produce side CB to Y, then ∠ABY is an exterior angle of ∆ABC at B.

Now, ∠ACB i.e., ∠3 is called the interior adjacent angle for ∠ACX at C, whereas ∠CBA and ∠CAB are called interior opposite angles for ∠ACX at C.

Similarly, ∠ABC i.e., ∠2 is called the interior adjacent angle for ∠ABY and ∠ACB, BAC are the interior opposite angles for ∠ABY.

Let us find a relation between the exterior angle and its interior opposite angles of a ∆ABC shown in the above figure.

In ∆ABC, Also, ∠1 + ∠ 2+ ∠3 = 180 deg; [Angle Sum Property]

Also, ∠ACB + ∠ACX = 180°; [Linear Pair]

⟹ ∠3 + ∠ACX = 180°

⟹ ∠3 + ∠ACX = ∠1 + ∠2 + ∠3; (Since, 1 + ∠2 + ∠3 = 180°)

⟹ ∠ACX = ∠1 + ∠2

Thus, exterior ∠ACX = sum of its two interior opposite angles, where ∠1 (= angle A) and ∠2 (= angle B) are the two interior opposite angles of the exterior ∠ACX

Similarly, exterior ∠ABY = ∠1 + ∠3

i.e. exterior ∠ABY = sum of its two interior opposite angles

Now, we have the following:

1. In a triangle, an exterior angle is equal to the sum of its two interior opposite angles.

2. In a triangle, an exterior angle is greater than either of the two interior opposite angles.

● Triangle.

Classification of Triangle.

Properties of Triangle.

Worksheet on Triangle.

To Construct a Triangle whose Three Sides are given.

To Construct a Triangle when Two of its Sides and the included Angles are given.

To Construct a Triangle when Two of its Angles and the included Side are given.

To Construct a Right Triangle when its Hypotenuse and One Side are given.

Worksheet on Construction of Triangles.

5th Grade Geometry Page

5th Grade Math Problems

From Properties of Triangle to HOME PAGE