Slope of a Line

We will discuss here about the slope of a line or gradient of a line.

Concept of slope (or gradient):

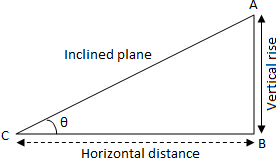
If θ (≠ 90°) is the inclination of a straight line, then tan θ is called its slope or gradient. The slope of any inclined plane is the ratio between the vertical rise of the plane and its horizontal distance.

i.e., slope = $\frac{vertical rise}{horizontal distance}$ = $\frac{AB}{BC}$ = tan θ

Where θ is the angle which the plane makes with the horizontal

Slope of a straight line:

The slope of a straight line is the tangent of its inclination and is denoted by letter ‘m’ i.e. if the inclination of a line is θ, its slope m = tan θ.

Note:

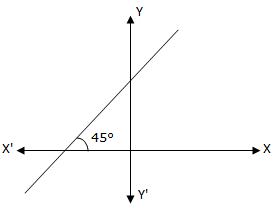
(i) The slope of a line is positive if it makes an acute angle in the anti-clockwise direction with x-axis.

Inclination θ = 45° Therefore, slope = tan 45° = 1

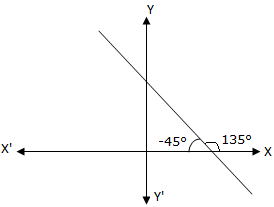
Inclination θ = 135° or -45° Therefore, slope = tan (-45°) = - tan 45° = -1

(ii) The slope of a line is negative, if it makes an obtuse angle in the anti-clockwise direction with the x-axis or an acute angle in the clockwise direction with the x-axis.

(iii) Since tan θ is not defined when θ = 90°, therefore, the slope of a vertical line is not defined. i.e., slope of y-axis is m = tan 90° = ∞ i.e., not defined.

(iv) Slope of x-axis is m = tan 0° = 0.

(v) Since the inclination of every line parallel to x-axis is 0°, so its slope (m) = tan 0° = 0. Therefore, the slope of every horizontal line is 0.

● Equation of a Straight Line

• Inclination of a Line
• Slope of a Line
• Intercepts Made by a Straight Line on Axes
• Slope of the Line Joining Two Points
• Equation of a Straight Line
• Point-slope Form of a Line
• Two-point Form of a Line
• Equally Inclined Lines
• Slope and Y-intercept of a Line
• Condition of Perpendicularity of Two Straight Lines
• Condition of parallelism
• Problems on Condition of Perpendicularity
• Worksheet on Slope and Intercepts
• Worksheet on Slope Intercept Form
• Worksheet on Two-point Form
• Worksheet on Point-slope Form
• Worksheet on Collinearity of 3 Points
• Worksheet on Equation of a Straight Line

10th Grade Math

From Slope of a Line to HOME