Equally Inclined Lines

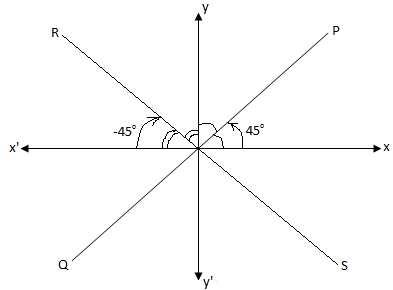
By the meaning of equally inclined lines, we mean that the lines which make equal angles with both the co-ordinate axes.

Equally Inclined Lines

The above diagram shows that PQ and RS are the two equally inclined lines.

From the above diagram it is clear that;

For PQ: Inclination θ = 45°,

Therefore, slope = tan 45° = 1.

For RS: Inclination θ = -45°,

Therefore, slope = tan (-45°) = -1.

Solved example on equally inclined lines:

Find the equation of the lines which is passes through the point (-2. 3) and equally inclined to the co-ordinate axes.

Solution:

From the above diagram it is clear that; there are two lines PQ and RS, equally inclined to the co-ordinate axes.

For line PQ: m = tan 45° = 1

and (x$_{1}$, y$_{1}$) = (-2, 3)

Therefore, its equation: y – y$_{1}$ = m(x – x$_{1}$)

⟹ y – 3 = 1(x + 2)

⟹ y - 3 = x + 2

⟹ y = x + 5

For line RS: m = tan (-45°) = -1

and (x$_{1}$, y$_{1}$) = (-2, 3)

Therefore, its equation: y – y$_{1}$ = m(x – x$_{1}$)

⟹ y – 3 = -1(x + 2)

⟹ y - 3 = -x - 2

⟹ y = -x + 1

Therefore, the required equations are y = x + 5 and y = -x + 1

10th Grade Math

From Equally Inclined Lines to HOME

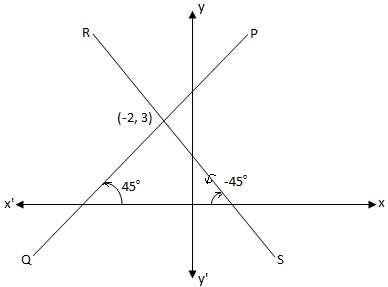
New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit