Section Formula

We will proof the definition of section formula.

Section of a Line Segment

Let AB be a line segment joining the points A and B. Let P be any point on the line segment such that AP : PB = λ : 1

Then, we can say that P divides internally AB is the ratio λ : 1.

Note: If AP : PB = m : n then AP : PB = \(\frac{m}{n}\) : 1 (since m : n = \(\frac{m}{n}\) : \(\frac{n}{n}\). So, any section by P can be expressed as AP : PB = λ : 1

Definition of section formula: The coordinates (x, y) of a point P divides the line segment joining A (x\(_{1}\), y\(_{1}\)) and B (x\(_{2}\), y\(_{2}\)) internally in the ratio m : n (i.e., \(\frac{AP}{PB}\) = \(\frac{m}{n}\)) are given by

x = (\(\frac{mx_{2} + nx_{1}}{m + n}\), y = \(\frac{my_{2} + ny_{1}}{m + n}\))

Proof:

Let X’OX and YOY’ are the co-ordinate axes.

Let A (x\(_{1}\), y\(_{1}\)) and B (x\(_{2}\), y\(_{2}\)) be the end points of the given line segment AB.

Let P(x, y) be the point which divides AB in the ratio m : n.

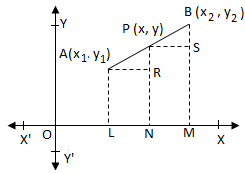
Then, \(\frac{AP}{PB}\) = \(\frac{m}{n}\))

We want to find the coordinates (x, y) of P.

Draw AL ⊥ OX; BM ⊥ OX; PN ⊥ OX; AR ⊥ PN; and PS ⊥ BM

AL = y\(_{1}\), OL = x\(_{1}\), BM = y\(_{2}\), OM = x\(_{2}\), PN = y and ON = x.

By geometry,

AR = LN = ON – OL = (x - x\(_{1}\));

PS = NM = OM – ON = (x\(_{2}\) -  x);

PR = PN – RN = PN – AL = (y - y\(_{1}\))

BS = BM – SM = BM – PN = (y\(_{2}\) - y)

Clearly, we see that triangle ARP and triangle PSB are similar and, therefore, their sides are proportional.

Thus, \(\frac{AP}{PB}\) = \(\frac{AR}{PS}\) = \(\frac{PR}{BS}\)

⟹ \(\frac{m}{n}\) = \(\frac{x - x_{1}}{x_{2} - x}\) = \(\frac{y - y_{1}}{y_{2} - y}\)

⟹ \(\frac{m}{n}\) = \(\frac{x - x_{1}}{x_{2} - x}\) and \(\frac{m}{n}\) = \(\frac{y - y_{1}}{y_{2} - y}\)

⟹ (m + n)x = (mx\(_{2}\) + nx\(_{1}\)) and (m + n)y = (my\(_{2}\) + ny\(_{1}\))

⟹ x = (\(\frac{mx_{2} + nx_{1}}{m + n}\) and y = \(\frac{my_{2} + ny_{1}}{m + n}\))

Therefore, the co-ordinates of P are  (\(\frac{mx_{2} + nx_{1}}{m + n}\),  \(\frac{my_{2} + ny_{1}}{m + n}\)).

● Distance and Section Formulae

• Distance Formula
• Distance Properties in some Geometrical Figures
• Conditions of Collinearity of Three Points
• Problems on Distance Formula
• Distance of a Point from the Origin
• Distance Formula in Geometry
• Section Formula
• Midpoint Formula
• Centroid of a Triangle
• Worksheet on Distance Formula
• Worksheet on Collinearity of Three Points
• Worksheet on Finding the Centroid of a Triangle
• Worksheet on Section Formula

10th Grade Math

From Section Formula to HOME