Proof of Pythagorean Theorem

The proof of Pythagorean Theorem in mathematics is very important.

In a right angle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

States that in a right triangle that, the square of a (a²) plus the square of b (b²) is equal to the square of c (c²).

In short it is written as: a² + b² = c²

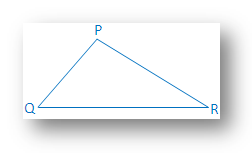
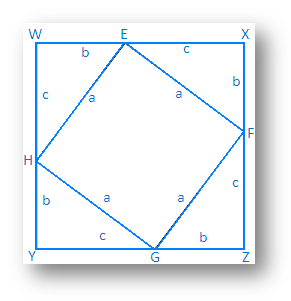
Let QR = a, RP = b and PQ = c. Now, draw a square WXYZ of side (b + c).  Take points E, F, G, H on sides WX, XY, YZ and ZW respectively such that WE = XF = YG = ZH = b.

Then, we will get 4 right-angled triangle, hypotenuse of each of them is ‘a’: remaining sides of each of them are band c. Remaining part of the figure is the

square EFGH, each of whose side is a, so area of the square EFGH is a².

Now, we are sure that square WXYZ = square EFGH + 4 ∆ GYF

or, (b + c)² = a² + 4 ∙ ¹/₂ b ∙ c

or, b² + c² + 2bc = a² + 2bc

or, b² + c² = a²

Proof of Pythagorean Theorem using Algebra:

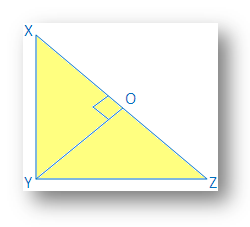
Given: A ∆ XYZ in which ∠XYZ = 90°.

To prove: XZ² = XY² + YZ²

Construction: Draw YO ⊥ XZ

Proof: In ∆XOY and ∆XYZ, we have,

∠X = ∠X                             → common

∠XOY = ∠XYZ                     →  each equal to 90°

Therefore, ∆ XOY ~ ∆ XYZ   → by AA-similarity

⇒ XO/XY = XY/XZ               

⇒ XO × XZ = XY² ----------------- (i)

In ∆YOZ and ∆XYZ, we have,

∠Z = ∠Z                                     →            common

∠YOZ = ∠XYZ                             →            each equal to 90°

Therefore, ∆ YOZ ~ ∆ XYZ           →            by AA-similarity

⇒ OZ/YZ = YZ/XZ                 

⇒ OZ × XZ = YZ² ----------------- (ii)

From (i) and (ii) we get,

XO × XZ + OZ × XZ = (XY² + YZ²)

⇒ (XO + OZ) × XZ = (XY² + YZ²)

⇒ XZ × XZ = (XY² + YZ²)

⇒ XZ ² = (XY² + YZ²)

Congruent Shapes

Congruent Line-segments

Congruent Angles

Congruent Triangles

Conditions for the Congruence of Triangles

Side Side Side Congruence

Side Angle Side Congruence

Angle Side Angle Congruence

Angle Angle Side Congruence

Right Angle Hypotenuse Side congruence

Pythagorean Theorem

Proof of Pythagorean Theorem

Converse of Pythagorean Theorem

7th Grade Math Problems

8th Grade Math Practice

From Proof of Pythagorean Theorem to HOME PAGE

Word problems on Pythagorean Theorem