Subscribe to our YouTube channel for the latest videos, updates, and tips.
Congruent Triangles
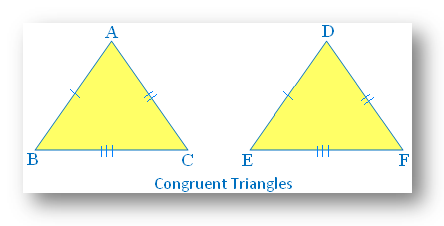
Congruent triangles are those two triangles which are said to be congruent if and only if one of them can be made to superpose on the other so as to cover it exactly.
Let ∆ABC and ∆DEF be two congruent triangles, then we can superpose ∆ABC on ∆DEF so as to cover it exactly. The vertices of ∆ABC fall on the vertices of ∆DEF in the following order A ↔ D, B ↔ E, C ↔ F.
Thus, the order in which vertices match automatically determines the correspondence between the sides and angles of the triangle. Corresponding parts are also called matching parts of triangles.
So, we have six equalities
Corresponding sides are congruent: AB = DE BC = EF CA = FD
Corresponding angles are congruent: ∠A = ∠D ∠B = ∠E ∠C = ∠F
In the congruent triangles we will observe six correspondences between their verities. The symbol used to denote correspondence is ‘↔’
A ↔ D B ↔ E C ↔ F written as ABC ↔ DEF
A ↔ E B ↔ F C ↔ D written as ABC ↔ EFD
A ↔ F B ↔ D C ↔ E written as ABC ↔ FDE
A ↔ D B ↔ F C ↔ E written as ABC ↔ DFE
A ↔ E B ↔ D C ↔ F written as ABC ↔ EDF
A ↔ F B ↔ E C ↔ D written as ABC ↔ FED
Therefore, ∆ABC ≅ ∆DEF
Note:
The order of letters in the name of two triangles will indicated the correspondence between the vertices of two triangles. Thus, two triangles are congruent only if there exist a correspondence between their vertices such that the correspondence sides and correspondence angles of two triangles are equal.
Conditions for the Congruence of Triangles
Right Angle Hypotenuse Side congruence
Converse of Pythagorean Theorem
7th Grade Math Problems
8th Grade Math Practice
From Congruent Triangles to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Calculating Profit Percent and Loss Percent | Profit and Loss Formulas
Jun 12, 25 12:48 PM
In calculating profit percent and loss percent we will learn about the basic concepts of profit and loss. We will recall facts and formula while calculating profit percent and loss percent. Now we wil -
Word Problems on Profit and Loss Worksheet |Cost Price |Selling Price
Jun 11, 25 04:26 PM
In word problems on profit and loss worksheet you will get different types of problems on cost price and selling price, profit and loss, calculating profit o loss, calculating selling price and cost p… -
Round off to Nearest 1000 |Rounding Numbers to Nearest Thousand| Rules
Jun 11, 25 03:12 PM
Round off to nearest 1000 is discussed here. While rounding off to the nearest 1000, if the digit in the hundreds place is between 0 – 4 i.e., < 5, then the hundreds place is replaced by ‘0’. If the d… -
Round off to Nearest 100 | Rounding Numbers To Nearest Hundred | Rules
Jun 11, 25 03:13 AM
While rounding off to the nearest hundred, if the digit in the tens place is between 0 – 4 i.e. < 5, then the tens place is replaced by ‘0’. If the digit in the units place is equal to or >5, then the… -
Round off to Nearest 10 |How To Round off to Nearest 10?|Rounding Rule
Jun 10, 25 05:36 PM
Round off to nearest 10 is discussed here. Rounding can be done for every place-value of number. To round off a number to the nearest tens, we round off to the nearest multiple of ten. A large number…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.