Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Congruent Angles
In congruent angles we will learn how to recognize that when two angles are congruent.
In case of two angles having the same vertex:
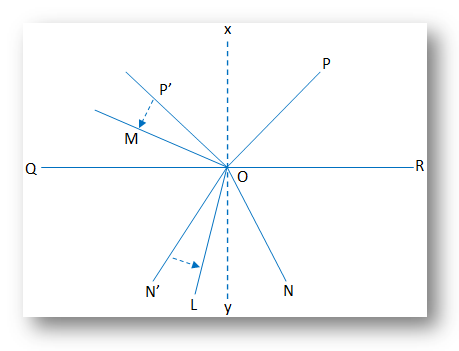
Suppose ∠LOM = ∠PON having same vertex O. Now we will verify their congruence.
A straight line QOR is drawn through point O and a
perpendicular xy is drawn on QOR at O.
With respect to the axis of reflection xy, ∠P’ON’ is the image of ∠PON. Now with centre of rotation O, OP’ is rotated through such an angle in anticlockwise direction, so that OP’ coincides with OM. Since ∠P’ON’ is rigid figure and equal to ∠LOM, ON’ falls on OL.
Therefore, ∠LOM ≅ ∠N’OP’ ≅ ∠NOP = ∠PON
With O as center of rotation, OP is rotated through such an angle (in anticlockwise direction) so that OP lies on OL. In the same manner ON being rotated equally, falls on OM.
Therefore, ∠LOM ≅ ∠PON
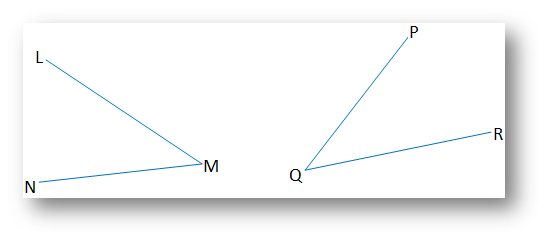
If two equal angles are at different positions but lie on the same plane.
∠LMN and ∠PQR are two equal angles at different positions but
lie on the same plane.
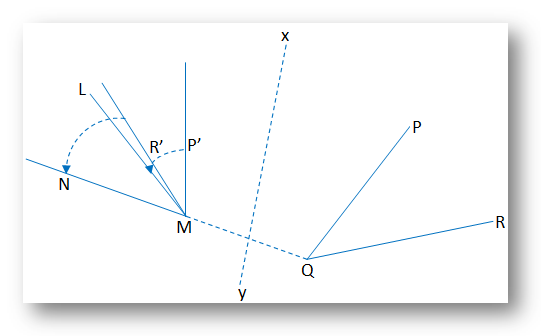
Taking xy, the perpendicular bisector of MQ as the axis of reflection, the image of ∠PQR is ∠P’MR’.
Therefore, ∠P’MR’ ≅ ∠PQR
Now observe that ∠LMN and ∠P’MR’ are two equal angles sharing common vertex M.
Conditions for the Congruence of Triangles
Right Angle Hypotenuse Side congruence
Converse of Pythagorean Theorem
7th Grade Math Problems
8th Grade Math Practice
From congruent angles to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
What is Area in Maths? | Units to find Area | Conversion Table of Area
Jul 17, 25 01:06 AM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla… -
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 17, 25 12:40 AM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
Formation of Square and Rectangle | Construction of Square & Rectangle
Jul 16, 25 11:46 PM
In formation of square and rectangle we will learn how to construct square and rectangle. Construction of a Square: We follow the method given below. Step I: We draw a line segment AB of the required… -
Perimeter of a Figure | Perimeter of a Simple Closed Figure | Examples
Jul 16, 25 02:33 AM
Perimeter of a figure is explained here. Perimeter is the total length of the boundary of a closed figure. The perimeter of a simple closed figure is the sum of the measures of line-segments which hav… -
Formation of Numbers | Smallest and Greatest Number| Number Formation
Jul 15, 25 11:46 AM
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.