Problems on Pyramid

Solved word problems on pyramid are shown below using step-by-step explanation with the help of the exact diagram in finding surface area and volume of a pyramid.

Worked-out problems on pyramid:

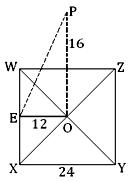
1. The base of a right pyramid is a square of side 24 cm. and its height is 16 cm.

Find:

(i) the area of its slant surface

(ii) area of its whole surface and

(iii) its volume. 

Solution:

Let, the square WXYZ be the base of the right pyramid and its diagonals WY and XZ intersect at O. If OP be perpendicular to the plane of the square at O, then OP is the height of the pyramid.

Draw OE ┴ WX

Then, E is the mid - point of WX. 

By question, OP = 16 cm. and WX = 24 cm. 

Therefore, OE = EX = 1/2 ∙ WX = 12 cm

Clearly, PE is the slant height of the pyramid. 

Since OP ┴ OE, hence from ∆ POE we get, 

PE² = OP² + OE² 

or,PE² = 16² + 12² 

or, PE² = 256 + 144 

or, PE² = 400

PE = √400

Therefore, PE = 20. 

Therefore, (i) the required area of slant surface of the right pyramid

= 1/2 × perimeter of the base × slant height. 

= 1/2 × 4 × 24× 20 square cm. 

= 960 square cm. 

(ii) The area of the whole surface of the right pyramid = area of slant surface + area of the base

= (960 + 24 × 24) square cm

= 1536 square cm.

(iii) the volume of the right pyramid

= 1/3 × area of the base × height

= 1/3 × 24 × 24 × 16 cubic cm 

= 3072 cubic cm.

2. The base of a right pyramid 8 m high, is an equilateral triangle of side 12√3 m. Find its volume and the slant surface.

Solution:

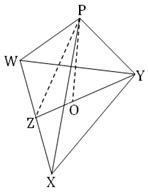
Let equilateral ∆ WXY be the base and P, the vertex of the right pyramid.

In the plane of the ∆ WXY draw YZ perpendicular to WX and let OZ = 1/3 YZ. Then, O is the centroid of ∆ WXY. Let OP be perpendicular to the plane of ∆ WXY at O; then OP is the height of the pyramid.

By question, WX = XY = YW = 8√3 m and OP = 8 m.

Since ∆ WXY is equilateral and YZ ┴ WX

Hence, Z bisects WX.

Therefore, XZ = 1/2 ∙ WX = 1/2 ∙ 12√3 = 6√3 m.

Now, from right - angled ∆ XYZ we get,

YZ² = XY² - XZ²

or, YZ² = (12√3) ² - (6√3)²

or, YZ² = 6² (12 - 3)

or, YZ² = 6² ∙ 9

or, YZ² = 6² ∙ 9

or, YZ² = 324

YZ = √324

Therefore, YZ = 18

Therefore, OZ = 1/3 ∙ 18 = 6.

Join PZ. Then, PZ is the slant height of the pyramid. Since OP is perpendicular to the plane of ∆ WXY at O, hence OP ┴ OZ .

Therefore, from the right angled ∆ POZ we get,

PZ² = OZ² + OP²

or, PZ ² = 6² + 8²

or, PZ² = 36 + 64

or, PZ² = 100

Therefore, PZ = 10

Therefore, the required slant surface of the right pyramid

= 1/2 × perimetre of the base × slant height

= 1/2 × 3 × 12√3 × PZ

= 1/2 × 36√3 × 10

= 180√3 square meter.

and its volume = 1/3 × area of the base × height

= 1/3 × (√3)/4 (12√3)² × 8

[Since, area of equilateral triangle

= (√3)/4 × (length of a side)² and height = OP = 8]

= 288√3 cubic meter.

● Mensuration

• Formulas for 3D Shapes
  
• Volume and Surface Area of the Prism
  
• Worksheet on Volume and Surface Area of Prism
  
• Volume and Whole Surface Area of Right Pyramid
  
• Volume and Whole Surface Area of Tetrahedron
  
• Volume of a Pyramid
  
• Volume and Surface Area of a Pyramid
  
• Problems on Pyramid
  
• Worksheet on Volume and Surface Area of a Pyramid
  
• Worksheet on Volume of a Pyramid

11 and 12 Grade Math 

From Problems on Pyramid to HOME PAGE