Prism

In prism we will discuss about what is prism along with the labeled figure of a prism, explanation about the right prism, formula of area of the side faces of a right prism, formula of total surface area of a right prism, formula of volume of a right prism and worked-out examples on volume and surface area of triangular prism, rectangular prism, right prism are explained using step-by-step explanation.

A prism is a solid bounded by a number of plane faces; its two faces, called the ends, are congruent parallel plane polygons and other faces, called the side faces (or lateral faces), are parallelograms.

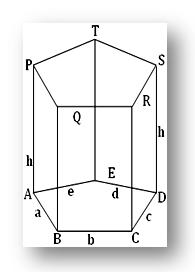
A prism has been displayed in the given figure ABCDE and PQRST are its two ends; these two are congruent parallel planes. The surfaces ABQP, BCRQ, CDSR etc. are its side faces and these faces are parallelograms. The number of such side faces is equal to the number of the sides of the polygon at the ends of the prism. A prism is said to be polygonal if its two ends are polygons. In particular, a prism is said to be triangular if its two ends are triangles; it is called quadrangular if its ends are quadrilaterals and so on. 

The straight line along which two adjacent side faces of a prism intersect is called a side-edge of the prism. These side-edges are all parallel and equal in length. The end on which a prism stands, is called its base. ABCDE is the base of the prism given in the figure. 

The perpendicular distance between two ends of a prism is called its height. 

Right Prism: If the side-edges of a prism are perpendicular to its ends (or to base), it is called a right prism ; otherwise, a prism is said to be oblique. 

For a right prism the side faces are all rectangles and each side-edge is equal its height.

The adjoining represents a right prism.

If h be the height (i.e., the perpendicular distance between the parallel end faces) and the lengths of the sides of the base polygon be a, b, c, d, . . . , then

(i) area of the side faces (i.e., lateral surfaces) of a right prism

= ah + bh + ch + ........

= (a + b + c + ....... ) ∙ h

= perimeter of the base × height;

(ii) area of total surfaces of a right prism

= area of its side faces + 2 × area of its base

(iii) volume of a right prism = ( area of base ) × (height).

Worked Out Examples:

1. The base of a right prism is a triangle whose sides arc of lengths 13 cm., 20 cm. and 21 cm. If the height of the prism be 9 cm. find the area of total lateral surface, area of the whole surface and the volume of the prism.

Solution: Let s be the semi-perimeter of the triangular base of the prism. Then,

S = (13 + 20 + 21)/2 cm. = 27 cm.

Therefore, the area of the prism = √[s(s - a)(s - b)(s - c)]

= √(27(27 - 13)(27 - 20)(27 - 21)) sq. cm.

= √(27 × 14 × 7 × 6) sq. cm.

= 9 × 7 × 2 sq. cm.

Therefore, the area of total lateral surface of the prism

= (perimeter of the base) × height

= (486 + 2 × 126) sq. cm. 

And the volume of the prism

= area of the base × height

= 126 × 9 cu.cm.

= 1134 cu.cm.

2. The volume of a right prism is 1320 cu. inches and its base trapezium whose parallel sides are of lengths 8 inches and I 4 inches. If the third side of the trapezium be perpendicular to the parallel sides and is of length 8 inches, find the height of the prism and the area of its lateral surface. 

Solution: Let the base of the right prism be the trapezium ABCD whose parallel sides are AB and DC and the third side DA is perpendicular to both AB and DC.

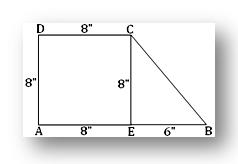
Draw CE perpendicular to AB. By question.

DC = 8, AB = 14 and DA = 8

Therefore, AE = DC = 8, CE = DA = 8

And EB = AB - AE = 14 – 8 = 6

Now , from the right - angled CEB we get,

BC² = CE² + EB² = 8² + 6² = 100

Or, BC = 10

Again, the area of trapezium ABCD 

= 1/2 × (sum of the lengths of the parallel sides) × (distance between the parallel sides)

= 1/2 × (AB + DC) × AD

= 1/2 (14 + 8) × 8

= 88 sq. inches.

Let h be the required height of the right prism. Then, volume of the prism = area of its base × its height.

or, 1320 = 88 × h [Since, volume of the prism = 1320 cu. Inches (given)]

Therefore, h = 1320/88 = 15.

Therefore the required height of the prism is 15 inches.

Again , the area of the lateral surface of the prism

= (perimeter of its base) × its height

= (AB + BC + CD + DA ) × 15

= (14 + 10 + 8 + 8) × 15

= 40 × 15

= 600 sq. inches.

3. The base of a right prism is a regular hexagon of side 8 cm. If the of the whole surface of the prism is 576√3 sq. cm., find its height. Also calculate volume of the prism.

Solution: We know that the area of a regular polygon of n sides is (na²/4) cot (π/n).

Where a is the length of the side of a polygon.

Therefore, (6 ∙ 8²)/4.cot (π/6) = 96√3 sq. cm.

i.e. , the area of the base of the prism = 96√3 sq. cm.

Let h cm. be the required height of the prism.

Now, the area of the whole surface of the prism.

= area of its lateral faces + 2 × area of its base

or, 576√3 = perimeter of the base × height of the prism + 2 × 96√3

or, 48h = 576√3 - 192√3 = 384√3

or, h = (384√3)/48 = 8√3

Therefore, the required height of the prism = 8√3cm.

The required volume of the prism

= area of its base × its height

= 96√3 × 8√3 c.c.

= 2304 c.c.


4. The base of a right prism Is a regular pentagon. If its height, volume and the area of lateral surface be h v and s respectively, prove that,
2Ovh = s²cot 36°.

Solution: Let a be the length of a side of the regular pentagon. Then, the area of base of the prism = area of the regular pentagon of side a.

= (5a²)/4 cot (π/5), [Since, area of a regular polygon of n sides = (na²)/4 cot (π/5)] 

= (5a²)/4 cot 36°.

Now, the volume of the prism = area of the base × height.

or, v = (5a²)/4 cot 36° × h

or, 4v = 5a²h cot 36°

Again, area of lateral surface of the prism = perimeter of the base × height of the prism

or , s = 5a × h

or, a = s/5h

Putting a = s/5h in (1) we get,

4v = 5 ∙ {s²/(25h)²} ∙ h ∙ cot 36°

or, 20vh = s² cot 36°. Proved


5. A right prism of height 12 cm. stands on a base which is a regular ,hexagon. If the area of the whole surface of the prism be 1152√3 sq.cm. find the volume of the prism.

Solution: Let a be the length of a side of the regular hexagon. Then, the area of side-faces of the prism

= 6a . 12 sq. cm. sq. cm. and the area of its base = area of the regular hexagon

= (6a²/4) cot (π/4), [since, the area of a regular polygon of n sides = (na²)/4 cot (π/5)]

= {(3√3)/2}a² sq. cm.

By problem, area of the whole surface of the prism = 1152√3

Therefore, 6a ∙ 12 + 2 ∙ {(3√3)/2}a² = 1152√3

Or, a² + 8√3 a - 384 = 0

Or, a² + 16√3 a - 8√3 a - 384 = 0

Or, a(a + 16√3) – 8√3 (a + 16√3 a) = 0

Or, (a + 16√3 a)(a - 8√3) = 0

Therefore, either, a = - 16√3 or, a = 8√3

Since a is positive , the value of a = -16√3 is admissible.

Therefore, we take a = 8√3

Therefore,the required volume,of the prism

= area of its base × its height

= (3√3)/2 ∙ (8√3)² ∙ 12 c.c.

= 3456√3 c.c.


6. The height of a right prism is 4 cm. and its volume 8 (√2 + 1) c.c. If the base a regular octagon, find the length of a side.

Solution: Let a cm. be the length of a side of the regular octagon. Then, the area of the base of the prism = area of the regular octagon

= (8a²/4) cot (π/8) [Since, the area of a regular polygon of n sides = (na²/4)cot (π/n)]

By question, the volume of the prism = 8 (√2 + 1)

or, area of the base of the prism × its height 8 (√2 + 1)

or, a² ∙ (√2 + 1) = √2 + 1 [Since, cot π/8 = cot 22¹/₂° = √2 + 1

or, a² = 1

or , a = 1 (Since, a > 0)

Therefore, the length of a side of the regular octagon is 1 cm.


7. Through an iron pipe whose cross-section is a rectangle of length 8cm. and breadth 5 cm., water flows uniformly at the rate 20 cm. per second. How long will it take to discharge 96 litre ?

Solution: Clearly, the volume of water discharged by the pipe per second = the volume of the prism whose height is 20 cm. and base is the rectangle having length 8cm. and breadth 5cm.

=Therefore, the required time to discharge 96 litre of water

= (96 litre)/(800 c.c.) seconds

= 2 minutes.


8. A vertical column, I5 metre high, has a square base on aside of 20 cm. Find the cost of painting its vertical surfaces at the rate of $ 2.25 per square metre.

Solution: Clearly, the area of the vertical surfaces = perimeter of the base × height of the column

= 4. (20/100) × 15 sq. metre = 12 sq. metre.

Therefore, the required cost of painting the vertical surfaces

= $ 12 × 2.25 = $ 27.

● Mensuration

• Formulas for 3D Shapes
  
• Volume and Surface Area of the Prism
  
• Worksheet on Volume and Surface Area of Prism
  
• Volume and Whole Surface Area of Right Pyramid
  
• Volume and Whole Surface Area of Tetrahedron
  
• Volume of a Pyramid
  
• Volume and Surface Area of a Pyramid
  
• Problems on Pyramid
  
• Worksheet on Volume and Surface Area of a Pyramid
  
• Worksheet on Volume of a Pyramid

11 and 12 Grade Math 

From Prism to HOME PAGE