Multiplying 2-Digit Number by 1-Digit Number
Here we will learn multiplying 2-digit number by 1-digit number. In two different ways we will learn to multiply a two-digit number by a one-digit number.
I: Examples of multiplying 2-digit number by 1-digit number without Regrouping:
We will have a quick review of multiplication of 2-digit number by 1-digit number without regrouping:
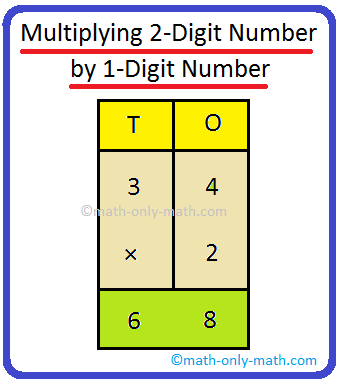
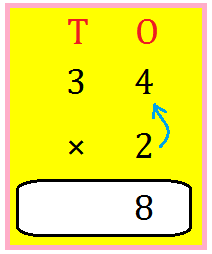
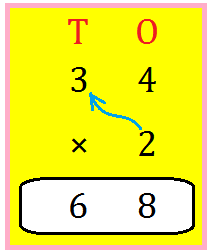
1. Multiply 24 by 2.
|
T O 2 4 × 2 4 8 |
First multiply the ones by 2. 4 × 2 = 8. Write 8 under O. Now multiply the tens by 2. 2 × 2 = 4. Write 4 under T. Thus, 24 × 2 = 48 |
2. Multiply 34 and 2
Solution:
|
Step I: Arrange the numbers vertically. Step II: First multiply the digit at the ones place by 2. 2 × 4 = 8 ones Step III: Now multiply the digit at the tens place by 2. 2 × 3 = 6 tens |
 Thus, 34 × 2 = 68 |
3. Multiply 20 by 3 by using expanded form
Solution:
20 → 2 tens + 0 ones
× 3 → × 3
6 tens + 0 ones
= 60 + 0
= 60
Therefore, 20 × 3 = 60
4. Multiply 50 by 1 by using short form
Solution:
50 → 50
× 1 → × 1
0 50
(i) First digit of one’s place is multiplied by 1, i.e., 0 × 1 = 0
(ii) Then digit at ten’s place is multiplied by 1, i.e., 5 tens × 1 = 5 tens
Hence, 50 × 1 = 50
5. Multiply 34 by 2.
We can multiply a given 2-digit number by a 1-digit number by vertical method.
Step I: Arrange the numbers in correct place.
Multiply the digit in the ones place by 2.
4 × 2 = 4 × 2 = 8 or 8 ones
Write 8 in the ones column.
Step II: Multiply the digit in the tens place by 2.
3 tens × 2 = 30 × 2 = 60 or 6 tens.
Write 6 in tens column.
So, 34 × 2 = 68
MULTIPLICATION OF A 2-DIGIT NUMBER BY A 1-DIGIT NUMBER WITHOUT REGROUPING:
6. Let us multiply 24 by 2.
Write the numbers one below the other as shown.
Step I: Multiply the ones digit by 2.
4 ones × 2 = 8 ones
Write 8 in the ones place.
Step II: Multiply the tens digit by 2.
2 tens × 2 = 4 tens
Write 4 in the tens place.
The product is 48.
Observe the following Example using Three Different Methods:
7. Multiply 13 by 2.
Solution:
First Method: Using Repeated Addition.
13 x 2 = 13 + 13 = 26
Therefore, 13 x 2 = 26.
Second Method: Using Expanded Form
Consider 13 as 10 + 3.
13 × 2 = (10 + 3) × 2
= 10 × 2 + 3 × 2
= 20 + 6
= 26.
Third Method: Short Form
Write the numbers according to place value shown on the right.
Step I:
Multiply the ones:
3 ones × 2 = 6 ones
Write 6 under ones column.
Step II:
Multiply the tens:
1 ten × 2 = 2 tens
Write 2 under tens column.
Thus, the product of 13 and 2 is 26.
II: Examples of multiplying 2-digit number by 1-digit number with Regrouping:
1. Multiply 66 by 3
|
T O 1 6 6 × 3 1 4 8 |
First multiply the ones by 3. 6 × 3 = 18 = one ten + 8 ones Write 8 under O. carry 1 ten Now multiply the tens by 3. 6 × 3 = 18 Add 1 to the product. 18 + 1 = 19 |
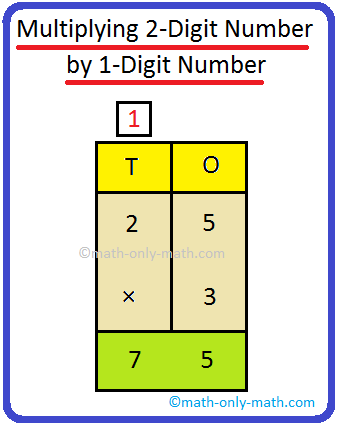
2. Multiply 25 by 3
|
Step I: Arrange the numbers vertically. Step II: First multiply the digit at the ones place by 3. 3 × 5 = 15 = 1 ten + 5 ones Write 5 in the ones column and carry over 1 to the tens column Step III: Now multiply the digit at the tens place by 3. 3 × 2 = 6 tens Now, 6 + 1 (carry over) = 7 tens |
 Thus, 25 × 3 = 75 |
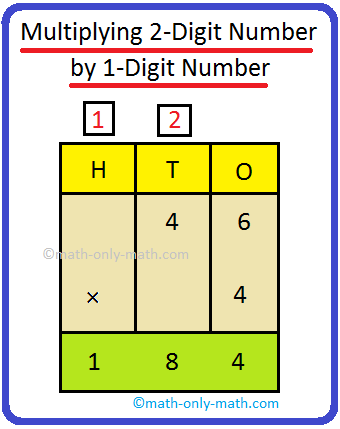
3. Multiply 46 by 4
|
Step I: Arrange the numbers vertically. Step II: Multiply the digit at the ones place by 4. 6 × 4 = 24 = 2 tens + 4 ones Write 4 in the ones column and carry over 2 to the tens column Step III: Now multiply the digit at the tens place by 4. 4 × 4 = 16 tens Now, 16 + 2 (carry over) = 18 tens = 1 hundred + 8 tens Write 8 at the tens place and 1 at the hundred place. |
 Thus,
46 × 4 = 184 |
4. Multiply 20 by 3 by using expanded form
Solution:
20 → 2 tens + 0 ones
× 3 → × 3
6 tens + 0 ones
= 60 + 0
= 60
Therefore, 20 × 3 = 60
5. Multiply 26 by 7 by using expanded form
Solution:
26 → 20 + 6 → 2 tens + 6 ones
× 7 → × 7 → × 7
(2 × 7) tens + (6 × 7) ones
2 tens + 6 ones
× 7 ones
14 tens + 42 ones
= 14 tens + (40 + 2) ones
= 14 tens + 4 tens + 2 ones
= 18 tens + 2 ones
= 180 + 2
= 182
Therefore, 26 × 7 = 182
6. Multiply 48 by 6 by using short form
Solution:
48
× 6
24 ← 48
= 28 tens 8 ones
= 288
Hence, 48 × 6 = 288
(i) 48 × 6 is written in column from.
(ii) 8 ones are multiplied by 6, i.e., 6 × 8 = 48 ones = 4 tens + 8 ones
8 is written is one’s column and 4 tens is gained.
(iii) Gained 4 is carried to the ten’s column.
(iv) Now 4 tens is multiplied by 6, i.e., 4 tens × 6 = 24 tens
(v) Carried 4 tens is added to 24 tens, i.e., 4 tens + 24 tens = 28 tens
7. Find the product of 58 × 5.
Solution:
58
× 5
25 ← 40
= 25 + 4 ← 0
= 29 0
= 290
(i) 8 ones × 5 = 40 = 4 tens + 0 one
(ii) 5 tens × 5 = 25 tens
(iii) 25 tens + 4 tens = 29 tens
Hence, 58 × 5 = 290
8. Multiply 37 by 8
Solution:
3 7
× 8
5 6
+ 2 4 0
2 9 6
(i) 7 ones × 8 = 56 ones = 5 tens 6 ones
56 is placed in such way that 5 comes under tens and 6 under ones
(ii) 3 tens × 8 = 24 tens = 240 ones
= 2 hundreds, 4 tens and 0 ones
240 is placed below 56 in such way that 2 comes under hundreds, 4 under tens and 0 under ones.
Hence, 37 × 8 = 296
Multiplication with Regrouping Once:
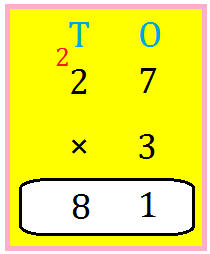
9. Let us multiply 27 by 3.
Write the numbers one below the other as shown.
Step I: Multiply the ones digit by 3.
7 ones × 3 = 21 ones
Regroup: 21 ones = 2 tens and 1 one
Write 1 in the ones place.
Carry over 2 tens and write it under T.
Step II: Multiply the tens digit by 3.
2 tens × 3 = 6 tens
Add 6 tens and 2 tens (carried over)
= 6 tens + 2 tens (carried over)
= 8 tens
Write 8 in the tens place.
The product is 81.
Multiplication with Regrouping Twice:
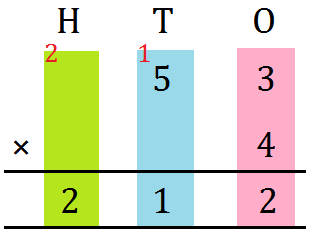
10. Let us multiply 53 by 4.
Write the numbers one below the other as shown.
Step I: Multiply the ones digit by 4.
3 ones × 4 = 12 ones
Regroup: 12 ones = 1 tens and 2 ones
Write 2 in the ones place.
Carry over 1 ten and write it under T.
Step II: Multiply the tens digit by 4.
5 tens × 4 = 20 tens
Add 20 tens and 1 ten (carried over)
= 20 tens + 1 ten = 21 tens
Regroup: 21 tens = 2 hundreds and 1 ten
Write 1 in the tens place.
Carry over 2 hundreds and write it under H.
Step III: Write 2 in the hundreds place.
The product is 212.
Word Problems on Multiplying a 2-digit Number by a 1-digit Number:
11. Robert can paint 45 pictures in a month. How many pictures can he paint in 3 months?
Step I: Multiply the digit in the ones place by 3. If the result is a 2-digit number, keep the ones and carry over the tens.
5 × 3 = 15
Keep 5 in the ones column and carry over 1 to the tens column.
Step II: Multiply the digit in the tens place by 3. Add the carried over number to the result. If it is a 2-digit number, keep the ones and carry over the tens to the hundreds column.
4 × 3 = 12
12 + 1 = 13
Keep 3 at the tens place and carry over 1 to the hundreds column.
Step III: Write the carried over digit in the hundreds column.
Thus, Robert can paint 135 pictures in 3 months.
Worksheet on Multiplying 2-Digit Number by 1-Digit Number:
Multiplication of 2-Digit Number by 1-Digit Number Without Regrouping:
I. Find the product:
(i) 23 × 3 =
(ii) 44 × 2 =
(iii) 33 × 2 =
(iv) 22 × 4 =
(v) 32 × 3 =
(vi) 40 × 2 =
(vii) 43 × 2 =
(viii) 12 × 3 =
(ix) 23 × 2 =
(x) 11 × 9 =
(xi) 21 × 4 =
(xii) 13 × 3 =
Answer:
I. (i) 69
(ii) 88
(iii) 66
(iv) 44
(v) 96
(vi) 80
(vii) 86
(viii) 36
(ix) 46
(x) 99
(xi) 84
(xii) 39
Multiplication of 2-Digit Number by 1-Digit Number With Regrouping:
II. Find the product:
(i) 46 × 2
(ii) 19 × 4
(iii) 27 × 3
(iv) 18 × 5
Answer:
II. (i) 92
(ii) 76
(iii) 81
(iv) 90
III. Multiply the following:
(i) 78 × 4
(ii) 63 × 6
(iii) 51 × 6
(iv) 39 × 8
(v) 72 × 9
(vi) 45 × 7
(vii) 17 × 4
(viii) 88 × 8
Answer:
III. (i) 312
(ii) 398
(iii) 306
(iv) 312
(v) 648
(vi) 315
(vii) 68
(viii) 704
IV. Solve the following:
(i) 37 × 6
(ii) 72 × 4
(iii) 56 × 7
(iv) 84 × 2
(v) 45 × 9
Answer:
IV. (i) 37 × 6
(ii) 72 × 4
(iii) 56 × 7
(iv) 84 × 2
(v) 45 × 9
V. Multiply the following :
|
(i) T O 3 1 × 2 _______ |
(ii) T O 4 7 × 1 _______ |
|
(iii) T O 1 1 × 3 _______ |
(iv) T O 2 2 × 2 _______ |
|
(v) T O 2 3 × 2 _______ |
(vi) T O 2 6 × 3 _______ |
|
(vii) T O 4 9 × 2 _______ |
(viii) T O 2 3 × 4 _______ |
|
(ix) T O 1 6 × 6 _______ |
(x) T O 1 9 × 5 _______ |
|
(xi) T O 5 2 × 5 _______ |
(xii) T O 2 3 × 6 _______ |
|
(xiii) T O 6 4 × 9 _______ |
(xiv) T O 3 2 × 7 _______ |
|
(xv) T O 7 5 × 8 _______ |
Answer:
III. (i) 62
(ii) 47
(iii) 33
(iv) 44
(v) 46
(vi) 78
(vii) 98
(viii) 92
(ix) 96
(x) 95
(xi) 260
(xii) 138
(xiii) 576
(xiv) 224
(xv) 600
VI. Multiply the following:
(i) 21 × 5 = _____
(ii) 34 × 2 = _____
(iii) 23 × 3 = _____
(iv) 27 × 3 = _____
(v) 38 × 2 = _____
(vi) 18 × 4 = _____
(vii) 25 × 8 = _____
(viii) 32 × 6 = _____
(ix) 29 × 4 = _____
(x) 45 × 5 = _____
Answer:
VI. (i) 105
(ii) 68
(iii) 69
(iv) 81
(v) 76
(vi) 72
(vii) 200
(viii) 192
(ix) 116
(x) 225
VII. Find the following products in your notebook.
|
(i) T O 2 9 × 7 _______ |
(ii) T O 6 3 × 4 _______ |
|
(iii) T O 3 8 × 7 _______ |
(iv) T O 6 6 × 4 _______ |
|
(v) T O 5 4 × 7 _______ |
(vi) T O 3 5 × 4 _______ |
|
(vii) T O 6 9 × 8 _______ |
(viii) T O 8 5 × 4 _______ |
|
(ix) T O 8 0 × 4 _______ |
(x) T O 5 8 × 8 _______ |
|
(xi) T O 5 1 × 7 _______ |
(xii) T O 6 3 × 8 _______ |
Answer:
VIII. (i) 203
(ii) 252
(iii) 266
(iv) 264
(v) 378
(vi) 140
(vii) 552
(viii) 340
(ix) 320
(x) 464
(xi) 357
(xii) 504
VIII. Find the products:
(i) 27 × 4 = __________
(ii) 5 × 10 = __________
(iii) 25 × 9 = __________
(iv) 16 × 4 = __________
(v) 14 × 8 = __________
(vi) 37 × 7 = __________
(vii) 63 × 4 = __________
(viii) 2 × 70 = __________
(ix) 53 × 5 = __________
Answer:
VIII. (i) 108
(ii) 50
(iii) 225
(iv) 64
(v) 112
(vi) 259
(vii) 252
(viii) 140
(ix) 265
IX. Word Problem on Multiplying 2-Digit Number by 1-Digit Number:
(i) A month has 30 days. How many days be there in 3 such months?
Answer:
IX. (i) 90 days
You might like these
2nd grade math Worksheets | Free Math Worksheets | By Grade and Topic
2nd grade math worksheets is carefully planned and thoughtfully presented on mathematics for the students.
2nd Grade Division Word Problems | Worksheet on Division Word Problems
Division is the opposite of multiplication. In 2nd Grade Division Word Problems we will learn how to solve different types of word problems problems on division.
2nd Grade Division Worksheet | Dividing 2-digit by 1-digit Numbers
In worksheet on 2nd grade division worksheet we will solve the multiple choice questions on division, problems on division fact for the repeated subtraction, terms used in division, division on the number line, facts about division, division of 2-digit number by 1-digit
Basic Division Facts | Division is the Inverse of Multiplication |Math
Some basic division facts are needed to follow for dividing numbers. The repeated subtraction of the same number is expressed by division in short form and in long form.
2nd Grade Multiplication Worksheet | 2-Digit by 1-Digit | 3-Digit by 1
In worksheet on 2nd grade multiplication worksheet we will solve the problems on fact about multiplication, multiplication on number line, terms used in multiplication, multiplication of 1-digit number by 1-digit number, multiplication of 2-digit number by 1-digit number
Multiplication and Division are Related | Multiplication Fact|Division
Does multiplication and division are related? Yes, multiplication and division both are related to each other. A few examples are given are given below to show how they are related to each other.
Divide on a Number Line | Various Division Problems | Solved Examples
How to divide on a number line? Learn to divide using number line to find the quotient. Solved examples to show divide on a number line: 1. Solve 14 ÷ 7 Solution: 7 is subtracted repeatedly
Divide by Repeated Subtraction | Division as Repeated Subtraction
How to divide by repeated subtraction? We will learn how to find the quotient and remainder by the method of repeated subtraction a division problem may be solved.
Concept of Multiplication | What is Multiplication? | Basics Math
Multiplication is repeated addition of a number to itself. Study the following example to understand it: Example: Take 3 groups of 2 pens each as shown below. How many pens are there in all?
Basic Multiplication Facts | Repeated Addition |Multiplication Process
Some basic multiplication facts are needed to follow for multiplying numbers. The repeated addition of the same number is expressed by multiplication in short.
Multiplication using Number Lines | Multiplying on a Number Line
The number line can be used for multiplication. Let us multiply 1-digit number using a number line. 1. Let us multiply 2 by 5 using a number line. Take 5 jumps of 2 steps each. Where do we reach? Start from 0. Take 5 jumps of 2 steps each. We reach 10. 2 + 2 + 2 + 2 + 2
Worksheet on Adding 2-Digit Numbers | 2-Digit Addition Problems | Ans
Practice the questions given in the worksheet on adding two digit Numbers. The questions are based on 2-digit addition problems that do not require regrouping (no regrouping) where 2 addends
Names of Three Digit Numbers | Place Value |2- Digit Numbers|Worksheet
How to write the names of three digit numbers? (i) The name of one-digit numbers are according to the names of the digits 1 (one), 2 (two), 3 (three), 4 (four), 5 (five), 6 (six), 7 (seven)
3-digit Numbers on an Abacus | Learning Three Digit Numbers | Math
We already know about hundreds, tens and ones. Now let us learn how to represent 3-digit numbers on an abacus. We know, an abacus is a tool or a toy for counting. An abacus which has three rods.
The Number 100 | One Hundred | The Smallest 3 Digit Number | Math
The greatest 1-digit number is 9 The greatest 2-digit number is 99 The smallest 1-digit number is 0 The smallest 2-digit number is 10 If we add 1 to the greatest number, we get the smallest number of the next series of numbers. So, if we add 1 to 99, we get 99 + 4 = 100.
From Multiplying 2-Digit Number by 1-Digit Number to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns
Dec 13, 24 08:43 AM
We see so many patterns around us in our daily life. We know that a pattern is an arrangement of objects, colors, or numbers placed in a certain order. Some patterns neither grow nor reduce but only r… -
Patterns in Math | Missing Number | Counting Numbers | Worksheets
Dec 13, 24 12:31 AM
Finding patterns in math is very important to understand the sequence in the series. We need to find the exact missing number that from the group of numbers. The counting numbers may be counting -
Concept of Pattern | Similar Patterns in Mathematics | Similar Pattern
Dec 12, 24 11:22 PM
Concept of pattern will help us to learn the basic number patterns and table patterns. Animals such as all cows, all lions, all dogs and all other animals have dissimilar features. All mangoes have si… -
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 12, 24 10:31 PM
2nd grade geometry worksheet -
Types of Lines |Straight Lines|Curved Lines|Horizontal Lines| Vertical
Dec 09, 24 10:39 PM
What are the different types of lines? There are two different kinds of lines. (i) Straight line and (ii) Curved line. There are three different types of straight lines. (i) Horizontal lines, (ii) Ver…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.