Methods of Prime Factorization
In prime factorization, we factorize the numbers into prime numbers, called prime factors.
Expressing a number as the product of its factors is called factorization.
For example, 48 = 2 × 24
Here, 48 in factorised.
There are many other forms of factorization of 48.
Such as 48 = 2 × 2 × 12
= 2 × 2 × 2 × 2 × 3
48 = 2 × 2 × 2 × 2 × 3, we see that each factor of 48 is a prime number.
It is called prime factorization.
When a number is expressed as a product of prime numbers, we call it prime factorization.
or
A factorization is which every factor is prime, is called the prime factorization of the number.
Prime factorization of 30 and 48 are given below:
30 = 2 × 3 × 5
48 = 2 × 2 × 2 × 2 × 3
To make the prime factorization of a number, we divide the given number by the prime number 2, 3, 5, 7, 11, etc., in this order repeatedly so long as the quotient is divisible by that number.
There are two methods of prime factorization:
Factorization means writing a given number as the product of two or more factors.
Prime factorization of a number is a way of showing a number as the product of prime numbers.
There are 2 methods to find the prime factors.
1. Division Method
2. Factor Tree Method
1. Prime Factorization by Division Method:
Observe the following steps.
I: First we divide the number by the smallest prime number which divides the number exactly.
II: We divide the quotient again by the smallest or the next smallest prime number if it is not exactly divisible by the smallest prime number. We repeat the process again and again till the quotient becomes 1. Remember, we use only prime numbers to divide.
III: We multiply all the prime factors. Remember, the product is the number itself.
Let us consider a few examples using division method.
1. Find the prime factors of 15.
First Step: 2 is the smallest prime number. But it cannot divide 15 exactly. So, consider 3.
Second Step: Now, 5 cannot be divide by 3. Consider the next smallest prime number 5.
The prime factors of 15 are 3 × 5.
2. Find the prime factors of 18.
First Step: Consider 2, the smallest prime number.
Second Step: As 9 cannot be divide by 2. Consider the next smallest prime 3. Repeat the process till quotient becomes 1.
The prime factors of 18 are 2 × 3 × 3.
2. Prime Factorization by Factor Tree Method
Observe the following steps.
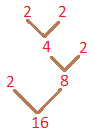
Suppose, we have to find the prime factors of 16
1. We consider the number 16 as the root of the tree.
2. We write a pair of factors as the branches of the tree i.e., 2 × 8 = 16
3. We further factorize the composite factor 8 as 4 and 2, and again the composite factors 4 as 2 and 2.
We repeat the process again till we get the prime factors of all the composite factors.
2 × 8 = 16
2 × 4 × 2 = 16
2 × 2 × 2 × 2 = 16
The prime factors of 16 = 2 × 2 × 2 × 2.
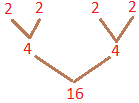
We can express the factor tree to find the prime factors of 16 in another way also.
4 × 4
2 × 2 × 2 × 2
The prime factors of 16 = 2 × 2 × 2 × 2.
Now, we will use both the methods (Factor Tree Method and Division Method) to the prime factorization of a number:
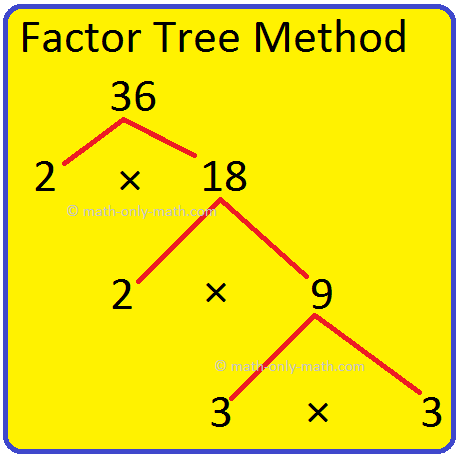
1. The prime factorization of 36
Factor Tree Method
Continue factorizing until only prime number remains.
36 = 2 × 2 × 3 × 3
Division Method
Continue diving unit the quotient is a prime.
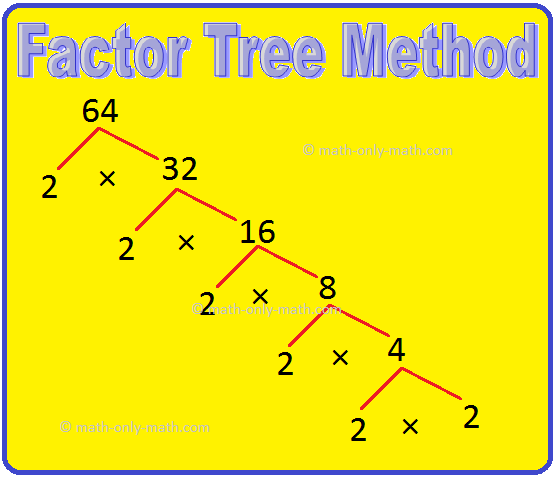
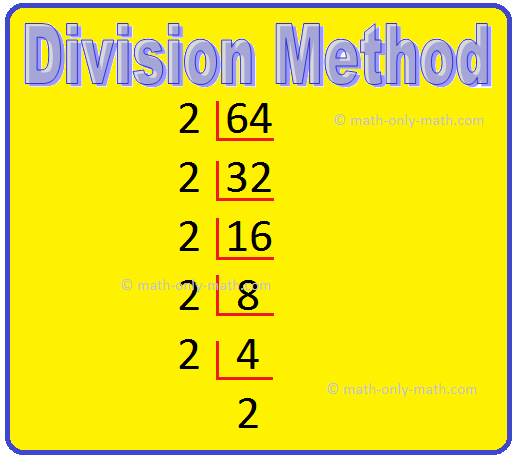
2. The prime factorization of 64.
Factor Tree Method
Continue factorizing until only prime number remains.
64 = 2 × 2 × 2 × 2 × 2 × 2
Division Method
Continue diving unit the quotient is a prime.
More Solved Examples on Methods of Prime Factorization:
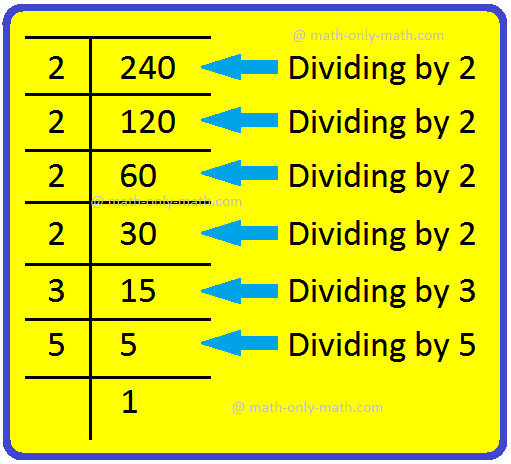
3. Express 240 as the product of prime numbers.
Division Method
Hence, 240 = 2 × 2 × 2 × 2 × 3 × 5
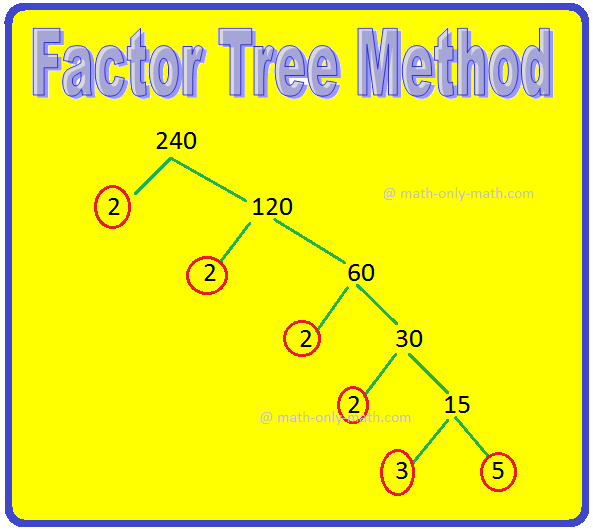
This process can be shown diagramatically, known as factor tree.
Factor Tree Method:
Therefore, 240 = 2 × 2 × 2 × 2 × 3 × 5
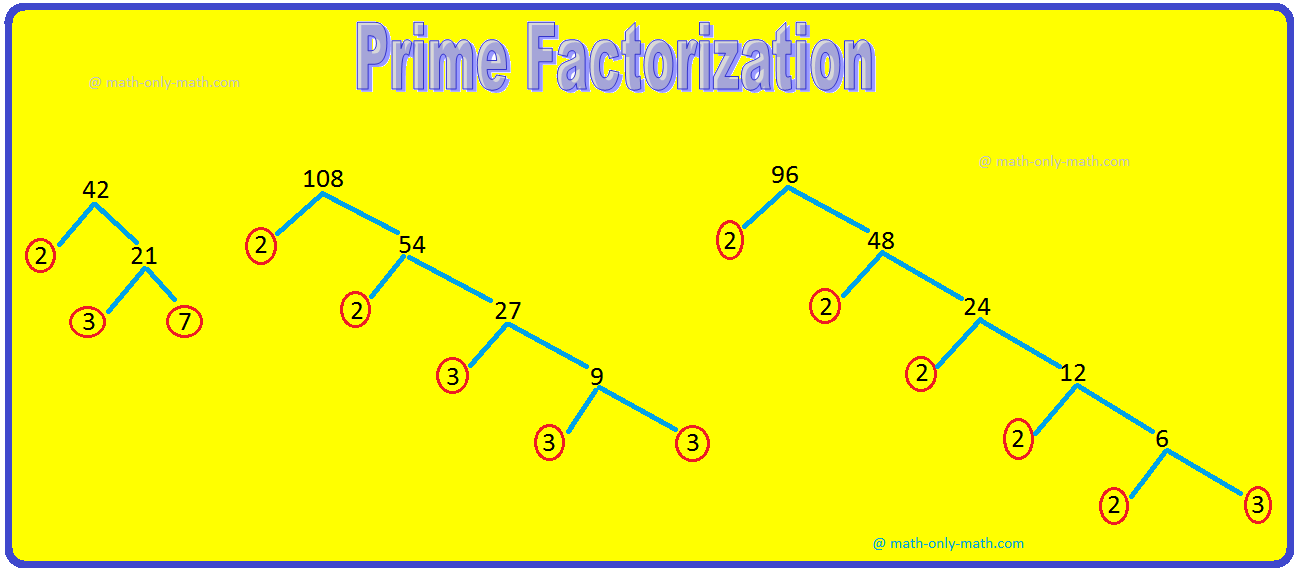
4. Draw a factor tree to show the prime factorization of 42, 96 and 108.
Therefore, 42 = 2 × 3 × 7
108 = 2 × 2 × 3 × 3 × 3
96 = 2 × 2 × 2 × 2 × 2 × 3.
Worksheet on Methods of Prime Factorization:
I. Prime factorize the following numbers using division method.
(i) 18
(ii) 125
(iii) 512
(iv) 144
(v) 360
(vi) 256
(vii) 96
(viii) 80
(ix) 625
(x) 169
Answer:
I. (i) 2 × 3 × 3
(ii) 5 × 5 × 5
(iii) 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
(iv) 2 x 2 x 2 x 2 x 3 x 3
(v) 2 × 2 × 2 × 3 × 3 × 5
(vi) 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
(vii) 2 × 2 × 2 × 2 × 2 × 3
(viii) 2 × 2 × 2 × 2 × 5
(ix) 5 × 5 × 5 × 5
(x) 13 × 13
II. Find the prime factors using the factor tree.
(i) 66
(ii) 75
(iii) 24
(iv) 156
(v) 128
Answer:
II. (i) 2 × 3 × 11
(ii) 3 × 5 × 5
(iii) 2 × 2 × 2 × 3
(iv) 2 × 2 × 3 × 13
(v) 2 × 2 × 2 × 2 × 2 × 2 × 2
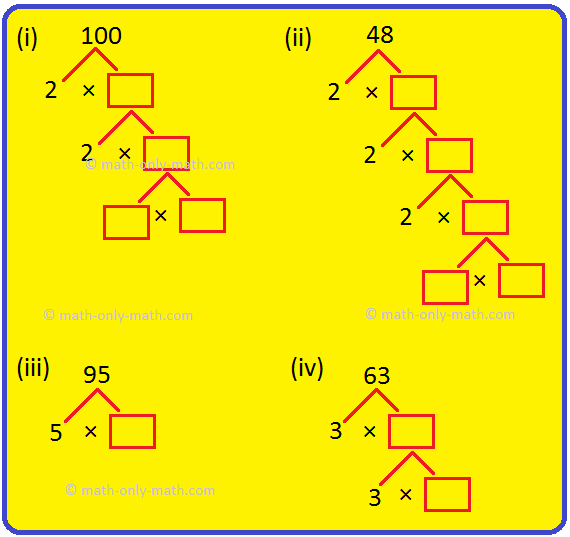
III. Copy and complete these factor trees.
Answer:
III. (i) 2 × 2 × 5 × 5
(ii) 2 × 2 × 2 × 2 × 3
(iii) 5 × 19
(iv) 3 × 3 × 7
IV. Write the prime factorization of 24.
Answer: Prime factorization of 24 = 2 × 2 × 2 × 3
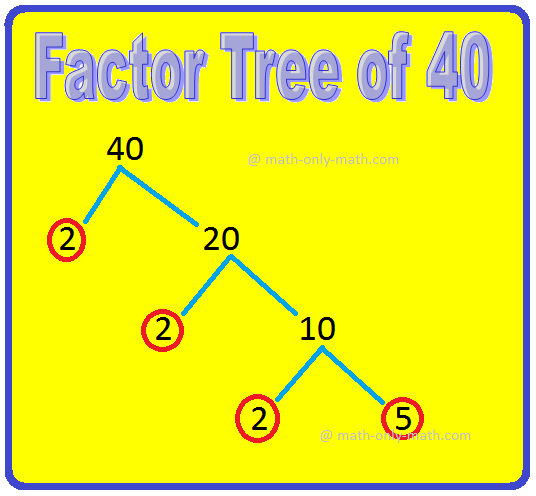
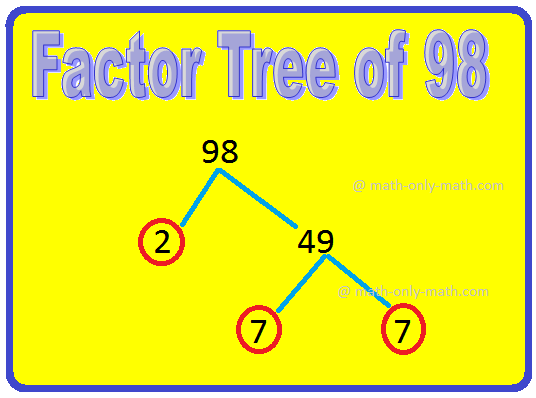
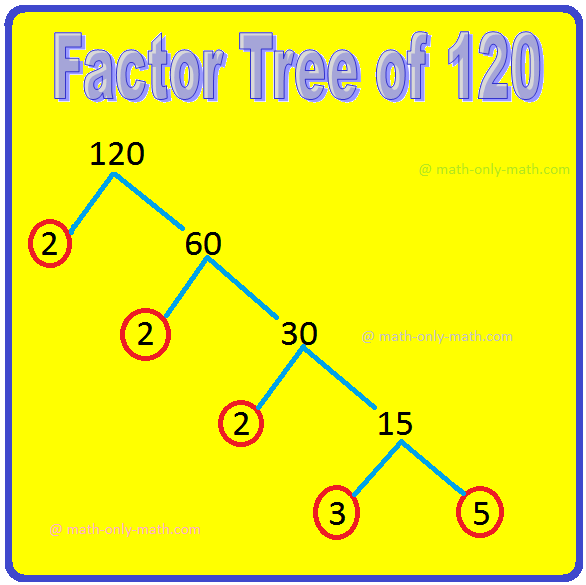
V. Draw a factor tree to show the prime factorisation of:
(i) 40
(ii) 98
(iii) 120
Answer:
V. (i)
(ii)
(iii)
VI. Write the prime factorization of 96.
Answer: Prime factorization of 96 = 2 × 2 × 2 × 2 × 2 × 3
You might like these
Terms Used in Division | Dividend | Divisor | Quotient | Remainder
The terms used in division are dividend, divisor, quotient and remainder. Division is repeated subtraction. For example: 24 ÷ 6 How many times would you subtract 6 from 24 to reach 0?
Successor and Predecessor | Successor of a Whole Number | Predecessor
The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number. For example, 9,99,99,999 is predecessor of 10,00,00,000 or we can also
Worksheets on Comparison of Numbers | Find the Greatest Number
In worksheets on comparison of numbers students can practice the questions for fourth grade to compare numbers. This worksheet contains questions on numbers like to find the greatest number, arranging the numbers etc…. Find the greatest number:
Number Worksheets | Practice Different Questions on Numbers | Answers
In number worksheets, students can practice different questions on numbers from printable free worksheets for grade 4 math on numbers. Write the number which is 1 more than 9? Write the number which
Comparison of Numbers | Compare Numbers Rules | Examples of Comparison
Rule I: We know that a number with more digits is always greater than the number with less number of digits. Rule II: When the two numbers have the same number of digits, we start comparing the digits from left most place until we come across unequal digits. To learn
Formation of Numbers | Smallest and Greatest Number| Number Formation
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,
Formation of Numbers with the Given Digits |Making Numbers with Digits
In formation of numbers with the given digits we may say that a number is an arranged group of digits. Numbers may be formed with or without the repetition of digits.
Formation of Greatest and Smallest Numbers | Arranging the Numbers
the greatest number is formed by arranging the given digits in descending order and the smallest number by arranging them in ascending order. The position of the digit at the extreme left of a number increases its place value. So the greatest digit should be placed at the
Place Value | Place, Place Value and Face Value | Grouping the Digits
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know that the position of a digit in a number determines its corresponding value
Expanded Form of a Number | Writing Numbers in Expanded Form | Values
We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its digits. This is shown here: In 2385, the place values of the digits are
Worksheet on Place Value | Place Value of a Digit in a Number | Math
Worksheet on place value for fourth grade math questions to practice the place value of a digit in a number. 1. Find the place value of 7 in the following numbers: (i) 7531 (ii) 5731 (iii) 5371
Worksheet on Expanded form of a Number | Expanded Form of a Number
Worksheet on expanded form of a number for fourth grade math questions to practice the expanded form according to the place values of its digit. 1. Write the expanded form of the following numbers
Examples on the Formation of Greatest and the Smallest Number |Example
In examples on the formation of greatest and the smallest number we know that the procedure of arranging the numbers in ascending and descending order.
Worksheet on Formation of Numbers | Questions on Formation of Numbers
In worksheet on formation of numbers, four grade students can practice the questions on formation of numbers without the repetition of the given digits. This sheet can be practiced by students
Rounding off Numbers | Nearest Multiple of 10 | Nearest Whole Number
Rounding off numbers are discussed here, where we need to round a number. (i) If we purchase anything and its cost is $12 and 23¢, the cost is rounded up to it’s nearest $ 12 and 23¢ is left. (ii) If we purchase another thing and its cost is $15.78. The cost is rounded up
From Methods of Prime Factorization to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Quarter Past and Quarter To | Quarter Past Hour | Quarter to Next Hour
Nov 23, 24 03:45 PM
The hands of clock move from left to right. This is called the clock wise motion. When the minute hand is on the right side of the clock, it shows the number of minutes past the hour. When the minute… -
Half Past an Hour | What does Half Past Mean? | Half an Hour|Half Past
Nov 23, 24 03:14 PM
We learnt that, one hour is equal to 60 minutes. When one hour is divided into two, it is half an hour or 30 minutes. The minute hand points at 6. We say, 30 minutes past an hour or half past an hour… -
Telling the Time | Teaching Time | Analogue Clock| Reading Time
Nov 23, 24 02:51 PM
Teaching time is an interactive activity for telling time. This activity helps students to learn how to read the clock to tell time using the analogue clock. While reading or observing the time on a -
2nd Grade Fractions Worksheet | Basic Concept of Fractions | Answers
Nov 23, 24 12:22 AM
In 2nd Grade Fractions Worksheet we will solve different types of problems on fractions, one-whole, one-half, one-third, one-fourth, three-fourth or s quarter. In a fraction, it is important that the… -
Time Duration |How to Calculate the Time Duration (in Hours & Minutes)
Nov 22, 24 12:34 AM
Time duration tells us how long it takes for an activity to complete. We will learn how to calculate the time duration in minutes and in hours. Time Duration (in minutes) Ron and Clara play badminton…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.