Worksheet on Functions or Mapping

Math worksheet on functions or mapping the questions are mainly related to domain, co-domain and range of functions.

1. Which of the following represent a mapping? 

(a) {(4, 2); (5, 3); (7, 5); (9, 7)} 

(b) {(2, 8); (3, 12); (4, 16)} 

(c) {(3, 7); (3, 11); (4, 9); (5, 11)} 

(d) {(1, 2); (2, 3); (3, 4); (4, 5)} 

(e) {(2, 1); (3, 1); (5, 1); (7, 1)} 

(f) {(1, 3); (1, 5); (2, 5)} 

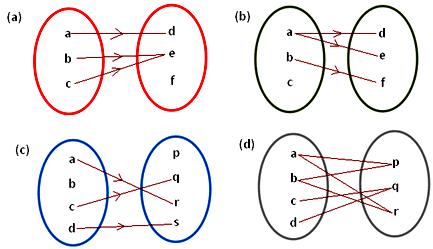
2. Which of the following arrow diagrams represent a mapping? 

Give reasons.

3. A function f is defined by f(x) = 2x - 3. Write the values of

(a) f(0)

(b) f(-2)

(c) f(3)

(d) f(-1)

4. Find the domain and range of each of the following functions.

(a) f(x) = 2 - x, x ∈ N

(b) f(x) = x² + 1, x ∈ W

(c) f(x) = x, x ∈ R

5. Let A = {1, 3, 5, 7) and B = {3, 5, 7, 9 11}

Consider the rule f(x) = x + 2, where x ∈ A.

Represent the mapping in the roster form.

Also, find the domain and range of the mapping.

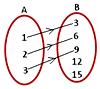
6. Let A = {1, 2, 3}     B = {3, 6, 9, 12, 15}

Draw the arrow diagram to represent the rule f(x) = 3x from A to B.

7. Let A = {3, 8, 11} and B = {1, 2, 3}

(a) Show that the relation R = {(3, 1), (8, 2)} is not a mapping from A to B.

(b) Show that the relation R = {(3, 1); (3, 3); (8, 2); (11, 1); (11, 3)} from A to B is not a mapping from A to B. 

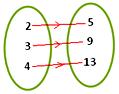
8. Let A = {2, 3, 4} and B = {5, 9, 13}

Consider the rule f(x) = 4x - 3, where x ∈ A

(a) Show that f is a mapping from A to B.

(b) Find the domain and range of the mapping.

(c) Represent the mapping in the roster form.

(d) Draw the arrow diagram to represent the mapping.

Answers for worksheet on functions or mapping are given below to check the exact answers of the questions. 

Answers:

1. (a), (b), (d), (e)

2. (a) Since, every element of the domain has a unique image in the co-domain.

3. (a) -3

(b) -7

(c) 3

(d) -5

4. (a) domain N Range= {1, 0, -1, -2...}

(b) Domain W Range = {1, 2, 5, 10, 17...}

(c) domain R Range R

5. F = {(1, 3) (3, 5) (5, 7) (7, 9)} Domain = {1, 3, 5, 7} Range = {3, 5, 7, 9}

6.

7. (a) domain {3, 8} ≠ A hence not a mapping

(b) Elements 3, 11 do not have unique image in B hence not a mapping

8. Ordered pairs {(2, 5), (3, 9), (4, 13)}

Elements of A have unique image in B hence a mapping

Domain {2, 3, 4} Range {5, 9, 13}

● Relations and Mapping

Ordered Pair

Cartesian Product of Two Sets

Relation

Domain and Range of a Relation

Functions or Mapping

Domain Co-domain and Range of Function

● Relations and Mapping - Worksheets

Worksheet on Math Relation

Worksheet on Functions or Mapping

7th Grade Math Problems

8th Grade Math Practice

From Worksheet on Functions or Mapping to HOME PAGE