Relation in Math

The concept of relation in math refers to an association of two objects or two variables based some property possessed by them.

For Example:

1. Rachel is the daughter of Noah. 

This statement shows the relation between two persons. 

The relation (R) being ‘is daughter of’. 


2. 5 is less than 9. 

This statement shows the relation between two numbers. 

The relation (R) being ‘is less than’. 

If A and B are two non-empty sets, then the relation R from A to B is a subset of A x B, i.e., R ⊆ A x B. 

If (a, b) ∈ R, then we write a R b and is read as 'a' related to 'b'. 

3. Let A and B denote the set animals and their young ones. 

Clearly, A = {cat, dog, cow, goat}

B = {kitten, puppy, calf, kid}

The relation (R) being ‘is young one of ‘.

Then the fact that,

Kitten is the young one of a cat.

Thus, kitten is related to cat.

Puppy is the young one of a dog.

Thus, puppy is related to dog.

Calf is the young one of a cow.

Thus, calf is related to cow.

Kid is the young one of a goat.

Thus, kid is related to goat.

This fact can also be written as set R or ordered pairs.

R = {(kitten, cat), (puppy, dog), (calf, cow), (kid, goat)}

Clearly, R ⊆ B × A

Thus, if A and B are two non-empty sets, then the relation R from A to B is a subset of A×B, i.e., R ⊆ A × B.

If (a, b) ∈ R, then we write a R b and is read as a is related to b.

Representation of Relation in Math:

The relation in math from set A to set B is expressed in different forms. 

      (i) Roster form 

      (ii) Set builder form 

      (iii) Arrow diagram 

i. Roster form: 

● In this, the relation (R) from set A to B is represented as a set of ordered pairs.

● In each ordered pair 1st component is from A; 2nd component is from B.

● Keep in mind the relation we are dealing with. (>, < etc.)

For Example:

1. If A = {p, q, r} B = {3, 4, 5}

then R = {(p, 3), (q, 4), (r, 5)}

Hence, R ⊆ A × B

2. Given A = {3, 4, 7, 10} B = {5, 2, 8, 1} then the relation R from A to B is defined as ‘is less than’ and can be represented in the roster form as R = {(3, 5) (3, 8) (4, 5), (4, 8), (7, 8)}

Here, 1ˢᵗ component < 2ⁿᵈ component.

In roster form, the relation is represented by the set of all ordered pairs belonging to R.

If A = {-1, 1, 2} and B = {1, 4, 9, 10}

if a R b means a² = b

then, R (in roster form) = {(-1, 1), (1, 1), (2, 4)

ii. Set builder form:

In this form, the relation R from set A to set B is represented as R = {(a, b): a ∈ A, b ∈ B, a...b}, the blank space is replaced by the rule which associates a and b.

For Example:

Let A = {2, 4, 5, 6, 8} and B = {4, 6, 8, 9}

Let R = {(2, 4), (4, 6), (6, 8), (8, 10) then R in the set builder form, it can be written as

R = {a, b} : a ∈ A, b ∈ B, a is 2 less than b}

iii. Arrow diagram:

● Draw two circles representing Set A and Set B.

● Write their elements in the corresponding sets, i.e., elements of Set A in circle A and elements of Set B in circle B.

● Draw arrows from A to B which satisfy the relation and indicate the ordered pairs.

For Example:



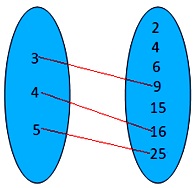
1. If A = {3, 4, 5} B = {2, 4, 6, 9, 15, 16, 25}, then relation R from A to B is defined as ‘is a positive square root of’ and can be represented by the arrow diagram as shown.
Here R = {(3, 9); (4, 16); (5, 25)}





In this form, the relation R from set A to set B is represented by drawing arrows from 1ˢᵗ component to 2ⁿᵈ components of all ordered pairs which belong to R.

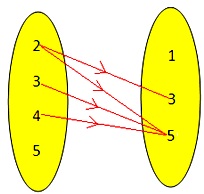
2. If A = {2, 3, 4, 5} and B = {1, 3, 5} and R be the relation 'is less than' from A to B,
then R = {(2, 3), (2, 5), (3, 5), (4, 5)}

● Relations and Mapping

Ordered Pair

Cartesian Product of Two Sets

Relation

Domain and Range of a Relation

Functions or Mapping

Domain Co-domain and Range of Function

● Relations and Mapping - Worksheets

Worksheet on Math Relation

Worksheet on Functions or Mapping

7th Grade Math Problems

8th Grade Math Practice

From Relation in Math to HOME PAGE