Worksheet on Math Relation

In worksheet on math relation we will solve different types of questions related to ordered pairs, Cartesian products of two sets, representation of math relation and also domain and range of a relation. Students can recapitulate the examples on math relation and then practice the questions given in the worksheet on math relation to get more ideas.

1. What can you say about the ordered pairs (a, b) and (b, a)? 

2. If (x + 2, y - 3) = (4, 3), find the values of x and y. 

3. If (x/3 + 1, y - 2/5) = (2, 3/5), find the values of x and y. 

4. If A = {p, q, r} and B = {a, b}, find A × B and B × A. Are the two products equal? 

5. If A × B = {(a, 1); (a, 2); (b, 1); (b, 2); (c, 1); (c, 2)}, find A and B. 

6. If P and Q are two sets, then P × Q consists of 6 elements. If three elements of p × Q are (3, 6); (4, 8); (5, 8), then find P × Q. 

7. If P × Q = {(x, 2); (x, 6); (x, 3); (y, 3); (y, 6); (y, 2)}, find Q × P.

8. If A = {1, 2, 3} and B = {4, 5, 6}, state which of the following is a relation from A to B.

(a) R₁ = {(1, 4); (2, 5); (6, 3)}     (b) R₂ = {(2, 5); (3, 6)}

(c) R₃ = {(6, 3); (5, 2); (4, 1)}     (d) R₄ = {(1, 5); (1, 6); (2, 4); (2, 6), (3, 4), (3, 5)}

9. Write the domain and range of the following relations.

(a) R₁ = {(4, 3); (6, 8); (4, 8); (0, 9); (7, 5); (0, 10)}

(b) R₂ = {(a, 2); (b, 3); (c, 2); (a, 3); (d, 4); (b, 4)}

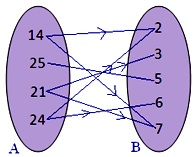
10. Let A = {14, 25, 21, 24} B = {2, 3, 5, 6, 7} be two sets and let R be a relation from A to B ‘is multiple of’.

  ● Represent the relation as a set of ordered pairs.

  ● Draw the arrow diagram for the same.

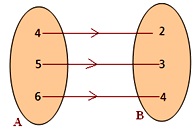
11. Adjoining figure shows a relationship between the set A and B. Write this relation in the roster form. What is its domain and range?

12. In the given ordered pairs (2, 8); (3, 9); (3, 5); (1, 7); (4, 24); (5, 25); (1, 1), find the following relationship:

  (a) Is a factor of ….

  (b) Is a square root of …..

  (c) Is 6 less than …..

Also, find the domain and range in each case.

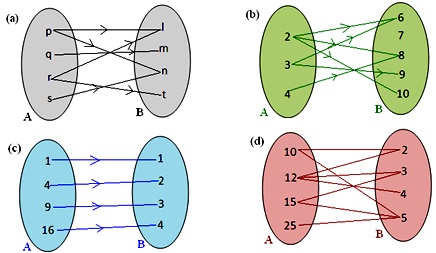
13. Draw the arrow diagrams to represent the following relations.

  (a) R₁ = {(3, 3); (3, 6); (3, 9); (5, 8); (6, 3)}

  (b) R₂ = {(4, 10); (4, 13); (4, 16); (5, 13); (6, 16)}

  (c) R₃ = {(2, 3); (3, 5); (4, 7); (5, 9); (6, 11)}

  (d) R₄ = {(p, l); (p, m); (q, x); (q, n); (r, m)}

14. Represent the following relation in the roster form.

Answers for worksheet on math relation are given below to make sure that the answers are correct after solving the questions.

Answers:

1. (a) (a, b) # (b, a)

2. x = 2, y = 6

3. x = 3, y = 1

4. A × B = {(p, a) (p, b) (q, a) (q, b) (r, a) (r, b)} and,

B × A = {(a, p) (b, p) (a, q) (b, q) (a, r) (b, r)}.
No.

5. A = {a, b, c} B = {1, 2}

6. P × Q = {(3, 6) (3, 8) (4, 6) (4, 8) (5, 6) (5, 8)}

7. Q × P = {(2, x) (2, y) (3, x) (3, y) (6, x) (6, y)}

8. (b) (d)

9. (a) Domain {0, 4, 6, 7} Range {3, 5, 8, 9, 10}

(b) Domain = {a, b, c, d} Range {2, 3, 4}

10. R = {(14, 2) (14, 7) (25, 5) (21, 3) (21, 7) (24, 2) (24, 3) (24, 6)}

11. R = {(4, 2) (5, 3) (6, 4)} Domain {4, 5, 6} Range {2, 3, 4}

12. (a) R = {(2, 8) (3, 9) (1, 7) (4, 24) (1, 1)} Domain {2, 3, 1, 4} Range {8, 9, 7, 24, 1}

(b) R = {(3, 9) (5, 25) (1, 1} Domain {1, 3, 5} Range {1, 9, 25}

(c) R = {(2, 8) (3, 9) (1, 7)} Domain {1, 2, 3} Range {7, 8, 9}

13.

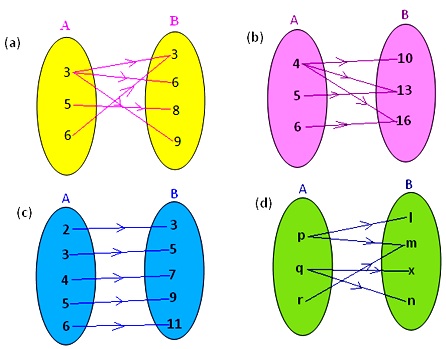
14. (a) R = {(p, l) (p, n) (q, m) (r, l) (r, t) (s, n)}

(b) R = {(2, 6) (2, 8) (3, 6) (3, 9) (4, 8) (2, 10)}

(c) R = {(1, 1) (4, 2) (9, 3) (16, 4)}

(d) R = {(10, 2) (10, 5) (12, 2) (12, 3) (12, 4) (15, 3) (15, 5) (25, 5)}

● Relations and Mapping

Ordered Pair

Cartesian Product of Two Sets

Relation

Domain and Range of a Relation

Functions or Mapping

Domain Co-domain and Range of Function

● Relations and Mapping - Worksheets

Worksheet on Math Relation

Worksheet on Functions or Mapping

7th Grade Math Problems

8th Grade Math Practice

From Worksheet on Math Relation to HOME PAGE