Square Root of Numbers in the Decimal Form
To find the square root of numbers in the decimal form are explained in the following steps:
Step I: Make the number of decimal places even by affixing a zero on the extreme right of the decimal part (if required).
Step II: In the integral part, mark the periods as done while finding the square root of a perfect square of some natural number.
Step III: In the decimal part, mark the periods on every pair of digits beginning with the first decimal place.
Step IV: Now, find the square root by long division method.
Step V: Put the decimal point in the square root as soon as the integral part is exhausted.
Examples on square root of numbers in decimal form:
1. Evaluate: √42.25
Solution:
Using the division method we may find the square root of the given number;
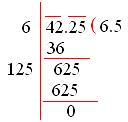
Therefore, √42.25 = 6.5
2. Evaluate: √1.96
Solution:
Using the division method we may find the square root of the given number;
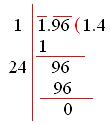
Therefore, √1.96 = 1.4
3. Evaluate: √6.4009
Solution:
Using the division method we may find the square root of the given number;
Therefore, √6.4009 = 2.53
4. Evaluate: √66.4225
Solution:
Using the division method we may find the square root of the given number;
Therefore, √66.4225 = 8.15
5. Evaluate: √0.4225
Solution:
Using the division method we may find the square root of the given number;
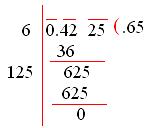
Therefore, √0.4225 = 0.65
● Square Root
Square Root of a Perfect Square by using the Prime Factorization Method
Square Root of a Perfect Square by Using the Long Division Method
Square Root of Numbers in the Decimal Form
Square Root of Number in the Fraction Form
Square Root of Numbers that are Not Perfect Squares
Practice Test on Square and Square Roots
● Square Root- Worksheets
Worksheet on Square Root using Prime Factorization Method
Worksheet on Square Root using Long Division Method
Worksheet on Square Root of Numbers in Decimal and Fraction Form
8th Grade Math Practice
From Square Root of Numbers in the Decimal Form to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.
Recent Articles
-
Half Past an Hour | What does Half Past Mean? | Half an Hour|Half Past
Nov 23, 24 03:14 PM
We learnt that, one hour is equal to 60 minutes. When one hour is divided into two, it is half an hour or 30 minutes. The minute hand points at 6. We say, 30 minutes past an hour or half past an hour… -
Telling the Time | Teaching Time | Analogue Clock| Reading Time
Nov 23, 24 02:51 PM
Teaching time is an interactive activity for telling time. This activity helps students to learn how to read the clock to tell time using the analogue clock. While reading or observing the time on a -
2nd Grade Fractions Worksheet | Basic Concept of Fractions | Answers
Nov 23, 24 12:22 AM
In 2nd Grade Fractions Worksheet we will solve different types of problems on fractions, one-whole, one-half, one-third, one-fourth, three-fourth or s quarter. In a fraction, it is important that the… -
Quarter Past and Quarter To | Quarter Past Hour | Quarter to Next Hour
Nov 22, 24 01:00 AM
The hands of clock move from left to right. This is called the clock wise motion. When the minute hand is on the right side of the clock, it shows the number of minutes past the hour. When the minute… -
Time Duration |How to Calculate the Time Duration (in Hours & Minutes)
Nov 22, 24 12:34 AM
Time duration tells us how long it takes for an activity to complete. We will learn how to calculate the time duration in minutes and in hours. Time Duration (in minutes) Ron and Clara play badminton…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.