Square Root of a Perfect Square by Using the Long Division Method

To find the square root of a perfect square by using the long division method is easy when the numbers are very large since, the method of finding their square roots by factorization becomes lengthy and difficult.

Steps of Long Division Method for Finding Square Roots:

Step I: Group the digits in pairs, starting with the digit in the units place. Each pair and the remaining digit (if any) is called a period.

Step II: Think of the largest number whose square is equal to or just less than the first period. Take this number as the divisor and also as the quotient.

Step III: Subtract the product of the divisor and the quotient from the first period and bring down the next period to the right of the remainder. This becomes the new dividend.

Step IV: Now, the new divisor is obtained by taking two times the quotient and annexing with it a suitable digit which is also taken as the next digit of the quotient, chosen in such a way that the product of the new divisor and this digit is equal to or just less than the new dividend. 

Step V: Repeat steps (2), (3) and (4) till all the periods have been taken up. Now, the quotient so obtained is the required square root of the given number.

Examples on square root of a perfect square by using the long division method

1. Find the square root of 784 by the long-division method.

Solution:

Marking periods and using the long-division method,

Therefore, √784 = 28

2. Evaluate √5329 using long-division method.

Solution:

Marking periods and using the long-division method,

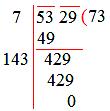
Therefore, √5329 =73

3. Evaluate: √16384.

Solution:

Marking periods and using the long-division method,

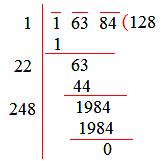
Therefore, √16384 = 128.

4. Evaluate: √10609.

Solution:

Marking periods and using the long-division method,

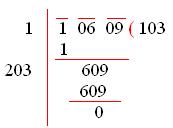
Therefore, √10609 = 103

5. Evaluate: √66049.

Solution:

Marking periods and using the long-division method,

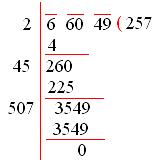
Therefore, √66049 = 257

6. Find the cost of erecting a fence around a square field whose area is 9 hectares if fencing costs $ 3.50 per metre.

Solution:

Area of the square field = (9 × 1 0000) m² = 90000 m²

Length of each side of the field = √90000 m = 300 m.

Perimeter of the field = (4 × 300) m = 1200 m.

Cost of fencing = $(1200 × ⁷/₂) = $4200.

7. Find the least number that must be added to 6412 to make it a perfect square.

Solution:

We try to find out the square root of 6412.

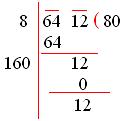
We observe here that (80)² < 6412 < (81)²

The required number to be added = (81)² - 6412

= 6561 – 6412

= 149

Therefore, 149 must be added to 6412 to make it a perfect square.

8. What least number must be subtracted from 7250 to get a perfect square? Also, find the square root of this perfect square.

Solution:

Let us try to find the square root of 7250.

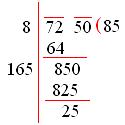
This shows that (85)² is less than 7250 by 25. 

So, the least number to be subtracted from 7250 is 25.

Required perfect square number = (7250 - 25) = 7225

And, √7225 = 85.

9. Find the greatest number of four digits which is a perfect square.

Solution

Greatest number of four digits = 9999.

Let us try to find the square root of 9999.

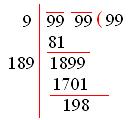
This shows that (99)² is less than 9999 by 198. 

So, the least number to be subtracted is 198.

Hence, the required number is (9999 - 198) = 9801.

10. What least number must be added to 5607 to make the sum a perfect square? Find this perfect square and its square root.

Solution:

We try to find out the square root of 5607.

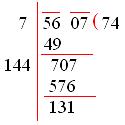
We observe here that (74)² < 5607 < (75)²

The required number to be added = (75)² - 5607

= (5625 – 5607) = 18

11. Find the least number of six digits which is a perfect square. Find the square root of this number.

Solution:

The least number of six digits = 100000, which is not a perfect square.

Now, we must find the least number which when added to 1 00000 gives a perfect square. This perfect square is the required number.

Now, we find out the square root of 100000.

Clearly, (316)² < 1 00000 < (317)²

Therefore, the least number to be added = (317)² - 100000 = 489.

Hence, the required number = (100000 + 489) = 100489.

Also, √100489 = 317.

12. Find the least number that must be subtracted from 1525 to make it a perfect square.

Solution:

Let us take the square root of 1525

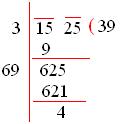
We observe that, 39² < 1525

Therefore, to get a perfect square, 4 must be subtracted from 1525.

Therefore the required perfect square = 1525 – 4 = 1521

● Square Root

Square Root

Square Root of a Perfect Square by using the Prime Factorization Method

Square Root of a Perfect Square by Using the Long Division Method

Square Root of Numbers in the Decimal Form

Square Root of Number in the Fraction Form

Square Root of Numbers that are Not Perfect Squares

Table of Square Roots

Practice Test on Square and Square Roots

● Square Root- Worksheets

Worksheet on Square Root using Prime Factorization Method

Worksheet on Square Root using Long Division Method

Worksheet on Square Root of Numbers in Decimal and Fraction Form

8th Grade Math Practice

From Square Root of a Perfect Square by Using the Long Division Method to HOME PAGE