Solid Shapes

We will discuss about basic solid shapes. We see a variety of solid objects in our surroundings. 

We know these objects. If we move them, lift them and touch them, they remain the same.

Objects around us, which do not change their shape easily, are called SOLIDS.

All these objects need space for storing them. We also call them Three-Dimensional (3-D) Shapes.

3-dimensional shape has 3 characteristics-length, width and height.

Look around and name the solids you see near you.

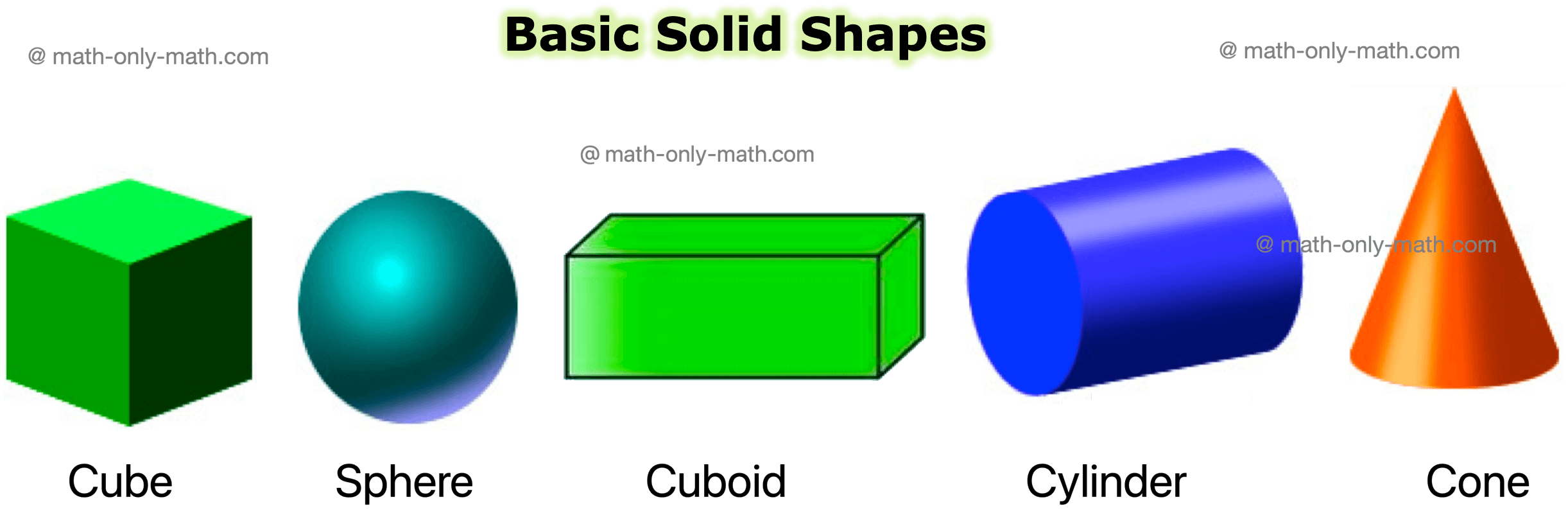
Solid objects have one or more shapes like the following.

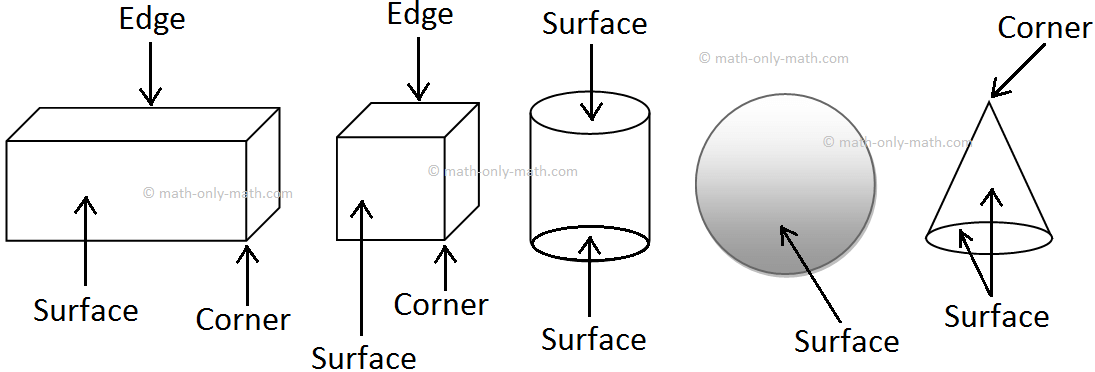
These are also called solid shapes. A solid shape has three parts:

Face: The surface of a solid is called its face.

Edge: The side of a solid is called an edge.

Corner: The point where the edges meet is called the corner or vertex.

We, now study some important solid shapes.

Faces, Edges, and Vertices of Solid Shapes:

A face is the surface of a solid. Two faces meet at an edge. Two edges meet at a point known as vertex (plural of vertex is vertices).

Solid Shapes:

This is a cube. A cube has 6 square faces. It has 12 edges. It has 8 corners.

This is a cuboid. A cuboid has 6 rectangular faces. It has 12 edges. It has 8 corners.

This is a cone. A cone has 1 flat face and a curved face. Cone has 1 corner.

This is a cylinder. A cylinder has 2 flat faces. It has 1 curved face. It has no corners.

This is a sphere. Sphere has no flat faces. Sphere has only a curved face. Sphere has no corners.

Solid shapes are fat but not flat like a sheet of paper.

This football is fat but not flat. So, it is a solid shape or a 3-D shape. This circle is flat. So, this is not a solid shape.

This circle is flat. So, this is not a solid shape.

A Cone is like a party hat or ice-cream.
A Sphere is like a bouncy ball.
A Cuboid is like this building.
A Cylinder is like a can.
A Cube is like a playing dice.

Let us learn

All shapes like a cuboid are called cuboidal shapes.

All shapes like a cylinder are called cylindrical shapes.

All shapes like a cone are called conical shapes.

All shapes like a sphere are called spherical shapes.

All shapes like a cube are called cubical shapes.

REMEMBER:

⚫ A plane surface is a completely flat surface.

For example, the top of your table, the blackboards, etc.

⚫ Those surfaces that have an inward bulging are known as curved surfaces.

For example, surface of an egg or the globe.

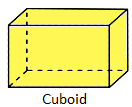
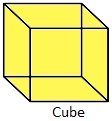
Basic Difference Between Cube and Cuboid:

Front, Back, Top and Bottom - 4 faces are same of one type. Left End, Right End - 2 same faces but different from other 4 faces.	It has 6 faces.               All six are of same type.

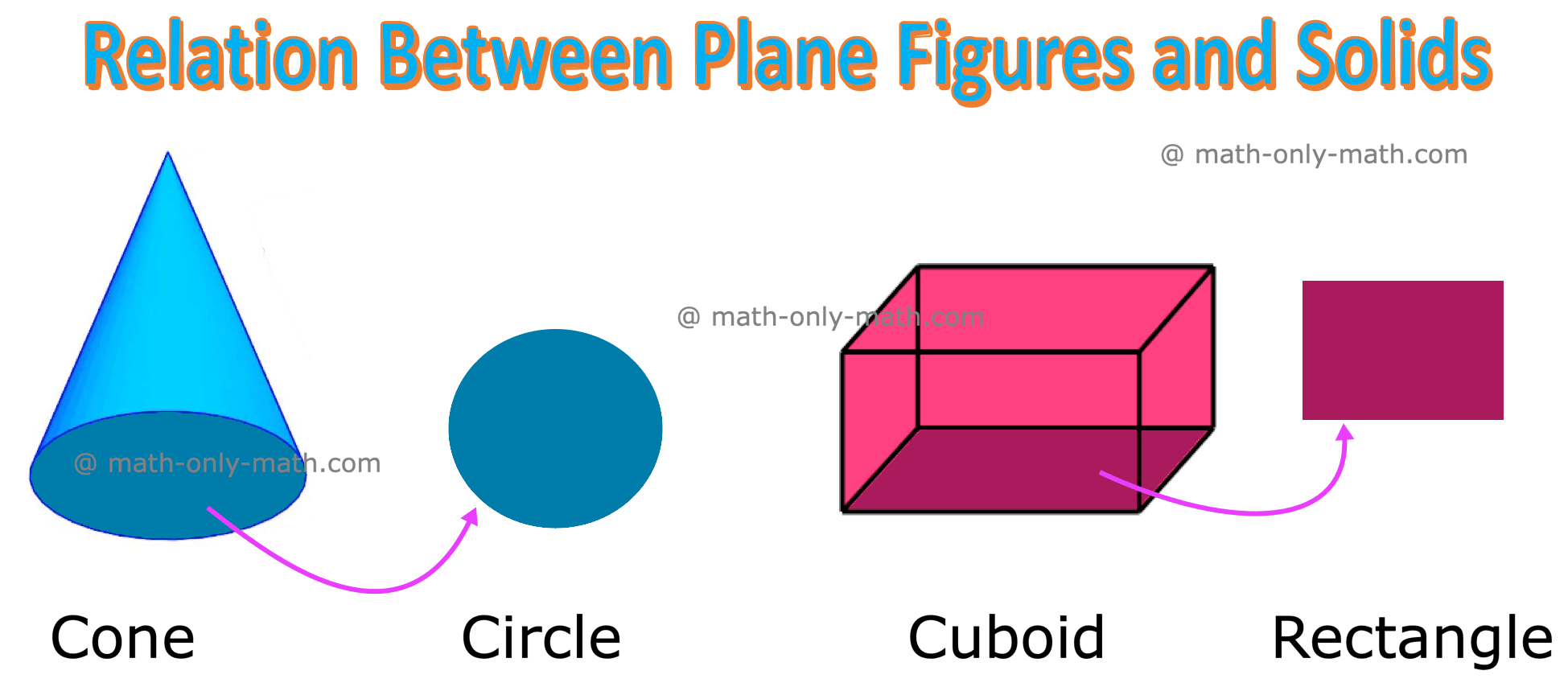
Relation between Plane Figures and Solids:

Plane figures and solids are related to each other.

For example, the base of a cone has the shape of a circle and the base of a cuboid has the shape of a rectangle.

Worksheet on Solid Shapes:

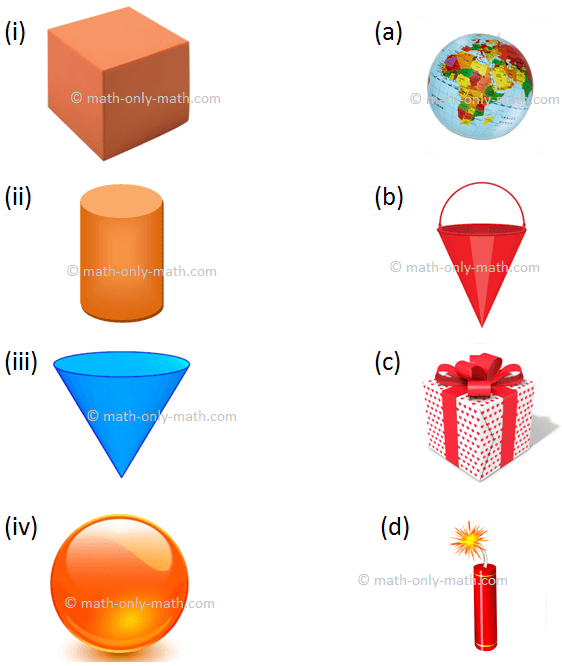
1. Match the objects with similar shape.

Answer:

1. (i) → (c)

(ii) → (d)

(iii) → (b)

(iv) → (a)

2. Match the shapes with their properties.

(i)

I am a solid shape. I have two flat faces.   I have one curved face.

(a)

(ii)

I am a plane shape. I have one curved side. I have no corners.

(b)

(iii)

I am a solid shape. I have six sides. All my sides are equal in length.

(c)

(iv)

I am a plane shape. I have four sides and four corners. My two opposite sides are equal.

(d)

(v)

I am a solid shape. I have one flat face and a curved face. I have one corner.

(e)

Answer:

2. (i) → (b)

(ii) → (d)

(iii) → (e)

(iv) → (a)

(v) → (c)

3. Write T for true and F for false statements.

(i) A cuboid has six faces.

(ii) A sphere has one face and one corner.

(iii) A carrot is cylindrical in shape.

(iv) A cylinder has three faces.

(v) A shuttlecock looks like a cone.

(vi) Every solid has at least one face.

(vii) Both a cylinder and a cone have three faces.

Answer:

3. (i) T

(ii) F

(iii) F

(iv) F

(v) T

(vi) T

(vii) F

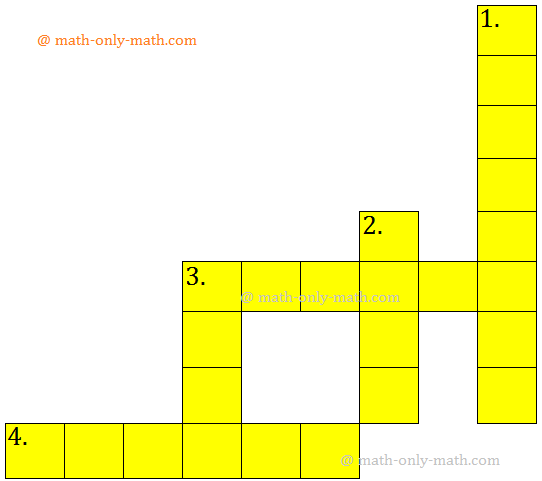
4. Mental Maths on Solid Shapes:

Complete the crossword with the name of the solid shapes.

Answer:

4. 

5. Identify the solid figure and then write the number of faces, edges and vertices. (The child should in fact take a concrete shape in hand and count.)

REMEMBER: Corner or vertex is a same thing.

(i)

Faces:      _____ Edges:     _____ Vertices:  _____

(ii)

Faces:      _____ Edges:     _____ Vertices:  _____

(iii)

Faces:      _____ Edges:     _____ Vertices:  _____

5. (i) Faces: 6

Edges: 12

Vertices: 8

(ii) Faces: 6

Edges: 12

Vertices: 8

(iii) Faces: 3

Edges: 2

Vertices: 0

6. Tick (✔) the correct choice:

(i) I have only 1 face. I am a cube/sphere.

(ii) I have eight corners. I am a cuboid/cone.

(iii) I have 3 faces. I am a sphere/cylinder.

(iv) I have one corner. I am a cone/cube.

(v) I have two edges. I am a cylinder/cone.

Answer:

6. (i) sphere.

(ii) cuboid

(iii) cylinder.

(iv) cone

(v) cylinder

7. Say whether 'Yes' or 'No':

Answer:

7. (i) No

(ii) Yes

(iii) Yes

(iv) No

(v) No

(vi) Yes

8. Answer True or False:

(i) A cube is a cuboid.

(ii) A cuboid is a cube.

(iii) The opposite faces of a cuboid are the same in size and shape.

(iv) All the faces of a cube are identical.

(v) All cube has eight faces.

(vi) There are no corners in a cylinder.

(vii) A sphere does not have any edge.

Answer:

8. (i) True

(ii) False

(iii) True

(iv) True

(v) False

(vi) True

(vii) True

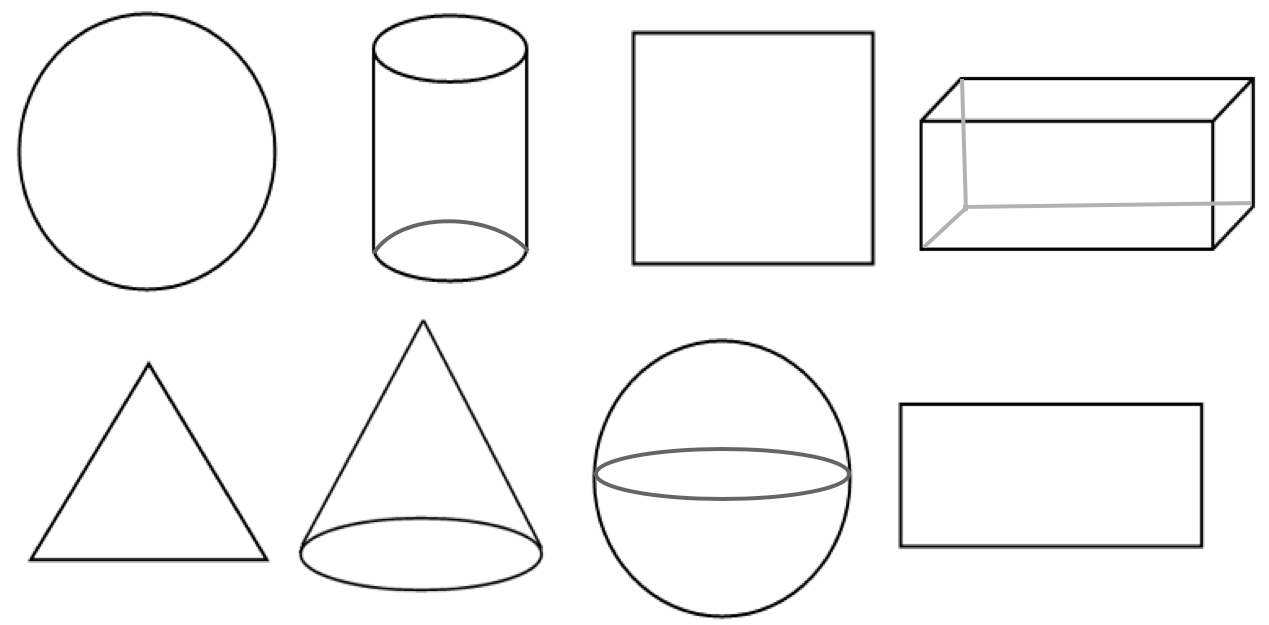
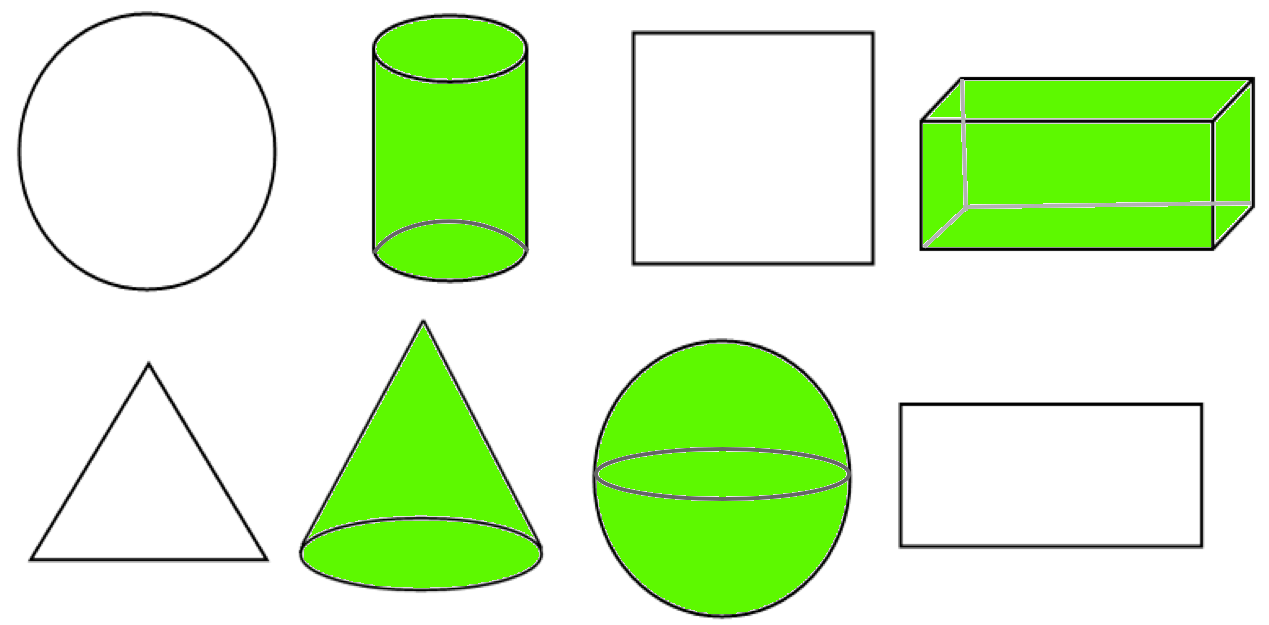
9. Look at the plane and solid shapes. Colour only the solid shapes in green.

Answer:

9.

9. Answer True or False:

(i) A cube is a cuboid.

(ii) A cuboid is a cube.

(iii) The opposite faces of a cuboid are the same in size and shape.

(iv) All the faces of a cube are identical.

(v) All cube has eight faces.

(vi) There are no corners in a cylinder.

(vii) A sphere does not have any edge.

Answer:

9. (i) True

(ii) False

(iii) True

(iv) True

(v) False

(vi) True

(vii) True

10. Name one object from your surroundings in the shape of a cube, cuboid, sphere, cone, and cylinder.

First Grade Math Activities

From Solid Shapes to HOME PAGE