Solid Geometry

Definitions on solid geometry terms:

(i) Dimension: Each of length, breadth and thickness of any body is called a dimension of the body. 

(ii) Point: A point has no dimension, that is, it has neither length nor breadth nor thickness ; it has position only. 

(iii) Line: A line has length only but no breadth and thickness. Therefore, a line has one dimension, that is, it is one dimensional. 

(iv) Surface: A surface has length and breadth but no thickness. Therefore, a surface has two dimensions, that is, it is two dimensional. 

(v) Solid: A solid has length, breadth and thickness. Therefore, a solid has three dimensions, that is, it is three dimensional. 

The book is a solid, each of its six faces is a surface, each of its edges is a line and each of its corners is a point.

A line is bounded by points, a surface is bounded by lines and a solid is bounded by surfaces. In other words, a line is generated by the motion of a point, a surface is generated by the motion of a line and a solid is generated by the motion of a surface.

(vi) Solid Geometry: The branch of geometry which deals with the properties of points, lines, surfaces and solids in three dimensional space is called solid geometry.

(vii) Plane or Plane Surface: If the straight line joining two points on a surface lies wholly on the surface then the surface is called a plane surface or a plane.

A straight line may be extended indefinitely in either direction, that is, straight lines are supposed to be of infinite length. Similarly, planes are also assumed to be of infinite extent, unless otherwise stated. The statement that a straight line lies wholly on a surface signifies that every point on the line (however produced in both directions) lies on the surface.

A surface is called curved surface when it is not a plane surface. 

(i) Lines or points are said to be co-planar if they lie on the same plane; in other words, lines or points are co-planar if a plane can be made to pass through them.

(ii) Two co-planar straight lines are either parallel or they intersect at a point. Two straight lines are said to be parallel when they are co-planar and they do not meet however indefinitely they are produced in both directions.

(iii) Two straight lines are said to be skew (or non-coplanar) if a plane cannot be made to pass through them. In other words, two straight lines are said to be skew when they do not meet at a point and they are not parallel.

(iv) Two planes are said to be parallel if they do not meet when extended infinitely in all directions.

(v) A straight line is said to be parallel to a plane if they do not meet when both are produced infinitely.

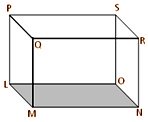
In the given picture we observe that, the lines LM, MN, NO and OL lie in the plane LMNO, that is, they are co-planar. The lines LM and LO meet at L and the lines LM and ON are parallel. LP and MN are skew lines and the line QR is parallel to the plane LPSO. The planes ABFE and DCGH are parallel.



A straight line is said to be perpendicular to a plane if it is perpendicular to every straight lines drawn in the plane through the point where the line meets the plane.

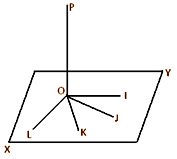
A straight line perpendicular to a plane is called a normal to the plane. In the given figure, the straight line OP meets the plane XY at O ; if OP is perpendicular to every straight lines OI, OJ, OK, OD etc. drawn through O in the XY plane then OP is perpendicular (or a normal) to the plane XY.




A straight line parallel to the direction of a plumb-line hanging freely at rest is called a vertical line. A plane which is perpendicular to a vertical line is called the horizontal plane. A straight line drawn in a horizontal plane is called a horizontal line.

Angle Between Two Skew Lines:

The angle between two skew lines (i.e., two non-co-planar straight lines) is

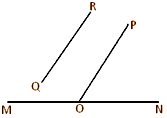
measured by the angle between one of them and a straight line drawn parallel to the other through a point on the first line. In the given figure, let MN and QR be two skew straight lines. Take any point O on the line MN and draw the straight line OP parallel to QR through O. Then ∠NOP gives the measure of the angle between the skew straight lines MN and QR.


A triangle is a plane figure since all its three sides lie in one plane. Similarly a parallelogram is also a plane figure. But a quadrilateral may or may not be plane figures since all its four sides always do not lie in one plane. A quadrilateral whose two adjacent sides lie in one plane and other two adjacent sides lie in a different plane is called a skew quadrilateral.

Orthogonal Projection:

(a) If a perpendicular be drawn from an external point on a given line then the foot of the perpendicular is called the orthogonal projection (or simply the projection) of the external point on the given line.

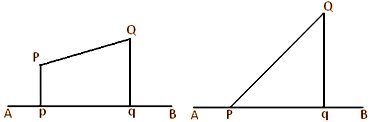
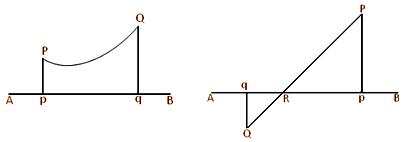
In the above left side figure, Pp is perpendicular from the external point P on the straight line AB. Since the foot of the perpendicular is p hence, p is the projection of P on the on the line AB. Again, we can observe that in the above right side figure, 5 the point P lies on the line AB ; hence, in this case the projection of P on AB is the point P itself.

(b) The locus of the feet of the perpendiculars drawn from all points of a line (straight or curved) on a given straight line is called the projection of the line on the given straight line.

In the above left side figure, Pp and Qq are perpendiculars from P and Q respectively on the straight line AB; p and q are the respective feet of perpendiculars. Then, pq is the projection of the straight line PQ on the straight line AB. Again, previous left hand side figure, the projection of the straight line PQ on the straight line AB is Pq. Again, similarly we can observe that in the above right side figure, pq is the projection of the curved line PQ on the straight line AB. Again, suppose the straight line PQ intersects the straight line AB at R; in this case, the projections of QR and RP on AB are qR and Rp respectively.

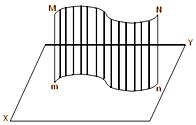
(c) The locus of the feet of the perpendiculars drawn from all points of a

line (straight or curved) on a given plane is called the projection of the line on the plane. In this figure, the locus of the feet of the perpendiculars drawn from points of the line MN on the plane XY is the line mn; hence, the projection of the line MN on the plane XY is the line mn.

Note: 

(i) The projection of a straight line on a plane is a straight line ; but the projection of a curved line on a plane may be a straight line as well as a curved line. If the curved line MN lies in a plane which is perpendicular to the plane XY then the projection of MN on the plane XY is a straight line.

(ii) A straight line and its projection on a plane are co-planar.

Angle Between a Straight Line and a Plane:

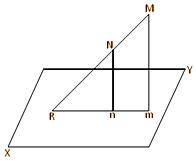
The angle between a straight line and a plane is measured by the angle between the given straight line and its projection on the given plane. Let mn be the projection of the straight line MN on the plane XY. Suppose, in the given figure, straight lines MN and mn (when produced) meet at the point R in the plane XY. Then the angle between the straight line MN and the plane XY is measured by ∠MRm.

Dihedral Angle:

The plane angle between two intersecting planes is called a dihedral angle between the planes. The angle between two intersecting planes (i.e., a dihedral angle) is measured as follows: Take any point on the line of intersection of the two planes. From this point draw two straight lines, one in each plane, at right angles to the line of intersection. Then the plane angle between the drawn two lines gives the measure of the dihedral angle between the planes.

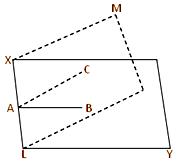
    Let XY and LM be two intersecting planes and XL be their line of intersection. From any point A on XL draw the straight line AB perpendicular to XL in the XY plane and the straight line AC perpendicular to XL in the LM plane. Then the plane ∠BAC is the measure of the dihedral angle between the two intersecting planes XY and LM.


 

If the dihedral angle between two intersecting planes is a right angle then one plane is said to be perpendicular to the other.

● Geometry

• Solid Geometry
• Worksheet on Solid Geometry
• Theorems on Solid Geometry
• Theorems on Straight Lines and Plane
• Theorem on Co-planar
• Theorem on Parallel Lines and Plane
• Theorem of Three Perpendiculars
• Worksheet on Theorems of Solid Geometry

11 and 12 Grade Math 

From Solid Geometry to HOME PAGE