Theorems on Solid Geometry

Some specific theorems on solid geometry are discussed here under this section.

Axioms:

The following two fundamental propositions may be considered as axioms:

Proposition 1: One and only one plane can be drawn through any two intersecting straight lines.

Proposition 2: Two intersecting planes cut one another in a straight line and in no other point outside the line of intersection.

The above two propositions lead to the following conclusions.

(a) A straight line intersects a plane at one point only or lies wholly in the plane or is parallel to the plane.

(b) Infinite number of planes can be drawn through a given straight line.

(c) The straight line joining two given points on a plane lies wholly in the plane if it be produced indefinitely in either direction. 

(d) The position of a plane is determined if it passes through 

(i) two intersecting straight lines; 

(ii) a given straight line and a given point outside the line; 

(iii) two parallel straight lines; 

(iv) three non-collinear points.

Example: Show that two parallel lines and any of its transversal lie in the same plane. 

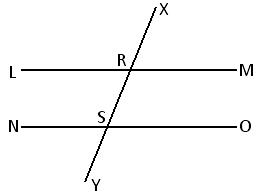
Let LM and NO be two parallel lines and XY, a transversal intersects LM at R and NO at S. We are to prove that the lines LM, NO and XY lie in the same plane (i.e., they are co-planar).

Proof: Since two parallel straight lines are co-planar, let us assume that the parallel tines LM and NO lie in the plane g. Now, the point R lies on the line LM and the point S on the line NO. Hence, it is evident that both the points R and S lie in the plane g. Therefore, the straight line joining the points R and S (i.e. the straight line XY) lies in the plane g.

Therefore, the straight lines LM, NO and XY lie in the same plane g.

Therefore, the straight lines LM, NO and XY are co-planar

● Geometry

• Solid Geometry
• Worksheet on Solid Geometry
• Theorems on Solid Geometry
• Theorems on Straight Lines and Plane
• Theorem on Co-planar
• Theorem on Parallel Lines and Plane
• Theorem of Three Perpendiculars
• Worksheet on Theorems of Solid Geometry

11 and 12 Grade Math 

From Theorems on Solid Geometry to HOME PAGE