Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Simultaneous Equations Graphically
How to solve a pair of simultaneous equations graphically?
In order to solve a pair of simultaneous equations graphically, we first draw the graph of the two equations simultaneously. We get two straight lines intersecting each other at a common point. This common point intersection of two lines gives the solution of the pair of simultaneous equations.
How to find the solution of simultaneous linear equations by graphing method?
Suppose the given system of linear equations is
p\(_{1}\)x + q\(_{1}\)y + r\(_{1}\) = 0 ------------- Equation (1)
p\(_{2}\)x + q\(_{2}\)y + r\(_{2}\) = 0 ------------- Equation (2)
Now draw the both given linear equations on a graph paper. Graph of linear equation is always a straight line.
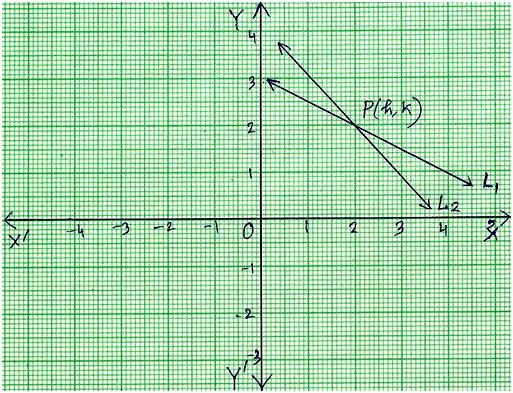
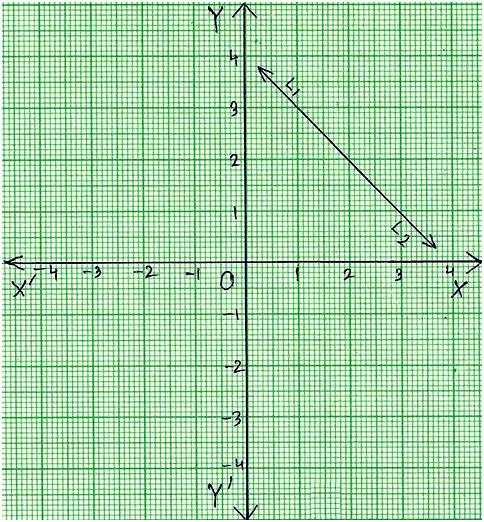
Let the line L\(_{1}\) represent the graph of p\(_{1}\)x + q\(_{1}\)y + r\(_{1}\) = 0
and L\(_{2}\) represent the graph of p\(_{2}\)x + q\(_{2}\)y + r\(_{2}\) = 0.
Then by solving the simultaneous equations graphically we can get three possible solutions.
1. When the two lines L\(_{1}\) and L\(_{2}\) intersect at a single point:
Then the two lines cross at a single point P (h, k), as shown in the graph.
Therefore, x = h and y = k is the unique solution of the given two equations.
This system is called independent.
Solved examples of a pairs of simultaneous equations graphically where the two lines intersect at a single point:
Solve graphically the system if linear equation x + y = 5 and x – y = 3.
Solution:
On a graph paper to solve simultaneous equations graphically, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis respectively.
x + y = 5 ------------ Equation (1)
Now convert the given equation in the form of y = mx + b
x + y = 5
⇒ x - x + y = - x + 5
⇒ y = - x + 5
Now we will apply the trial and error method to find 3 pairs of values of (x, y) which satisfy the given equation y = -x + 5.
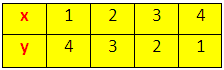
When the value of x = 1 then y = -1 + 5 = 4
When the value of x = 2 then y = -2 + 5 = 3
When the value of x = 3 then y = -3 + 5 = 2
When the value of x = 4 then y = -4 + 5 = 1
Arrange these value of the linear equation y = -x + 5 in the table 1.Table 1
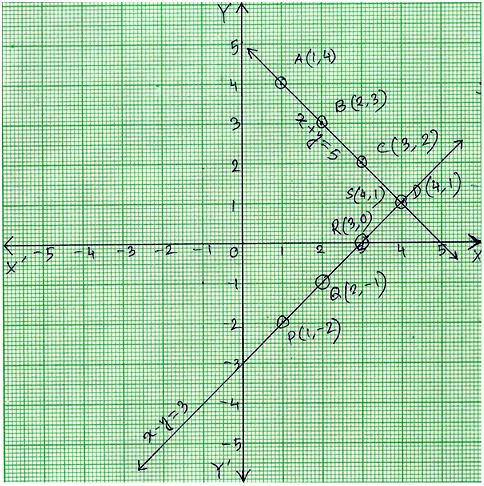
Now plot the points of the equation x + y = 5; A (1, 4), B (2, 3), C (3, 2), D (4, 1) on the graph paper.
Join the points of A, B, C and D; to get the graph line AD.
Thus line AD is the graph of x + y = 5.
x – y = 3 ------------ Equation (2)
Now convert the given equation in the form of y = mx + b
x – y = 3
⇒ x – x – y = – x + 3
⇒ -y = -x + 3
⇒ y = x – 3
Now we will apply the trial and error method to find 3 pairs of values of (x, y) which satisfy the given equation y = x - 3.
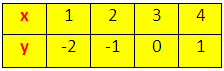
When the value of x = 1 then y = 1 – 3 = -2
When the value of x = 2 then y = 2 – 3 = -1
When the value of x = 3 then y = 3 – 3 = 0
When the value of x = 4 then y = 4 – 3 = 1
Arrange these value of the linear equation y = x - 3 in the table 2.Table 2
Now plot the points of the equation x – y = 3; P (1, -2), Q (2, -1), R (3, 0), S (4, 1) on the graph paper.
Join the points of P, Q, R and S; to get the graph line PS.
Thus line PS is the graph of x – y = 3.
We get two straight lines intersecting each other at (4, 1).
Therefore, x = 4 and y = 1 is the solution of the given system of equation.
2. When the two lines L\(_{1}\) and L\(_{2}\) are coincident:
Then the two equations actually be the same line, as shown in the graph.
Therefore, the given two equations have infinitely many solutions.
This system is called dependent.
Solved examples of a pairs of simultaneous equations graphically where the two lines coincidentally be the same line:
Solve graphically the system if linear equation 3x - y = 2 and 9x – 3y = 6.
Solution:
On a graph paper to solve simultaneous equations graphically, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis respectively.
3x - y = 2 ------------ Equation (1)
Now convert the given equation in the form of y = mx + b
y = 3x - 2
Now we will apply the trial and error method to find 3 pairs of values of (x, y) which satisfy the given equation y = 3x - 2.
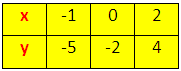
When the value of x = -1 then y = 3(-1) - 2 = -5
When the value of x = 0 then y = 3(0) - 2 = -2
When the value of x = 2 then y = 3(2) - 2 = 4
Table 1
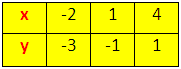
Now plot the points of the equation 3x - y = 2; A (-1, -5), B (0, -2), C (2, 4) on the graph paper.
Join the points of A, B and C; to get the graph line AC.
Thus line AC is the graph of 3x - y = 2.
9x – 3y = 6 ------------ Equation (2)
Now convert the given equation in the form of y = mx + b
y = (9x – 6)/3
⇒ y = 9x/3 – 6/3
Now we will apply the trial and error method to find 3 pairs of values of (x, y) which satisfy the given equation y = 9x/3 – 6/3.
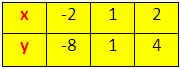
When the value of x = -2 then y = -8
When the value of x = 1 then y = 1
When the value of x = 2 then y = 4
Arrange these value of the linear equation y = 9x/3 – 6/3 in
the table 2.
Table 2
Now plot the points of the equation 9x – 3y = 6; P (1, -2), Q (2, -1), R (3, 0) on the graph paper.
Join the points of P, Q and R; to get the graph line PR.
Thus line PR is the graph of 9x – 3y = 6.
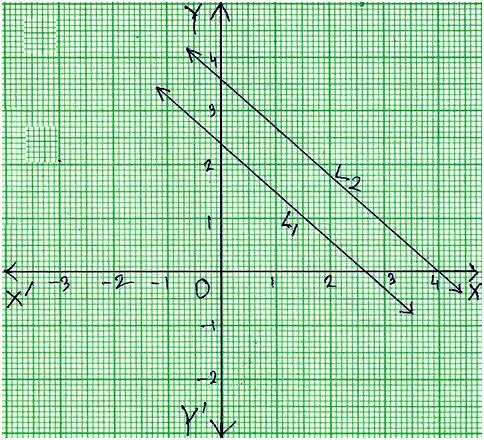
We find that the two straight lines AC and PR coincides each other.
Therefore, the given system of equations has an infinite number of solutions.
3. When the two lines L\(_{1}\) and L\(_{2}\) are parallel:
Then the two equations have no common solutions, as shown in the graph.
This system is called inconsistent.
Solved examples of a pairs of simultaneous equations graphically when the two lines are parallel:
Solve graphically the system if linear equation 2x - 3y = 5 and 6y – 4x = 3.
Solution:
On a graph paper to solve simultaneous equations graphically, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis respectively.
2x - 3y = 5 ------------ Equation (1)
Now convert the given equation in the form of y = mx + b
2x - 3y = 5
⇒ 3y = (2x – 5)
⇒ y = (2x – 5)/3
Now we will apply the trial and error method to find 3 pairs of values of (x, y) which satisfy the given equation y = (2x – 5)/3
When the value of x = -2 then y = -3
When the value of x = 1 then y = -1
When the value of x = 4 then y = 1
Arrange these value of the linear equation y = (2x – 5)/3 in the table 1.
Table 1
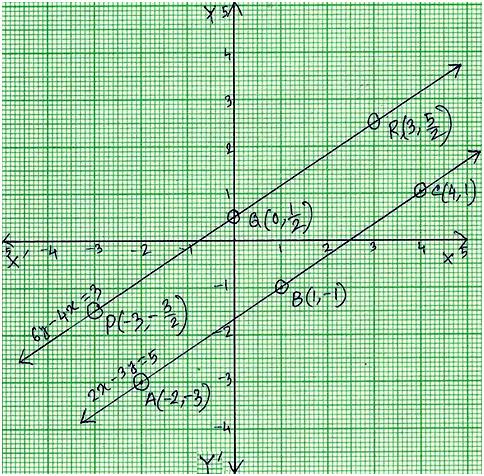
Now plot the points of the equation 2x - 3y = 5; A (-2, -3), B (1, -1) and C (4, 1) on the graph paper.
Join the points of A, B and C; to get the graph line AC.
Thus line AC is the graph of 2x - 3y = 5.
6y – 4x = 3 ------------ Equation (2)
Now convert the given equation in the form of y = mx + b
6y – 4x = 3
⇒ 6y = (3 + 4x)
⇒ y = (3 + 4x)/6
Now we will apply the trial and error method to find 3 pairs of values of (x, y) which satisfy the given equation y = (3 + 4x)/6.
When the value of x = -3 then y = -3/2
When the value of x = 0 then y = 1/2
When the value of x = 3 then y = 5/2
Arrange these value of the linear equation y = (3 + 4x)/6 in the table 2.
Table 2
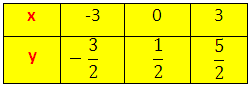
Now plot the points of the equation 6y – 4x = 3; P (-3, -3/2), Q (0, 1/2), R (3, 5/2) on the graph paper.
Join the points of P, Q and R; to get the graph line PR.
Thus line PR is the graph of 6y – 4x = 3.
We get from the graph that two straight lines are parallel to each other.
Therefore, the given system of equations has no solutions.
Thus we conclude that to solve a pair of simultaneous equations graphically then the possible outcomes can be:
(i) a unique solution if the graph lines intersect at a point.
(ii) infinitely many solutions if the two graph lines coincides.
(iii) no solution if the two graph lines are parallel.
Related Concepts:
● Ordered pair of a Coordinate System
● Find the Coordinates of a Point
● Coordinates of a Point in a Plane
● Plot Points on Co-ordinate Graph
● Simultaneous Equations Graphically
● Graph of Perimeter vs. Length of the Side of a Square
● Graph of Area vs. Side of a Square
● Graph of Simple Interest vs. Number of Years
7th Grade Math Problems
8th Grade Math Practice
From Simultaneous Equations Graphically to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
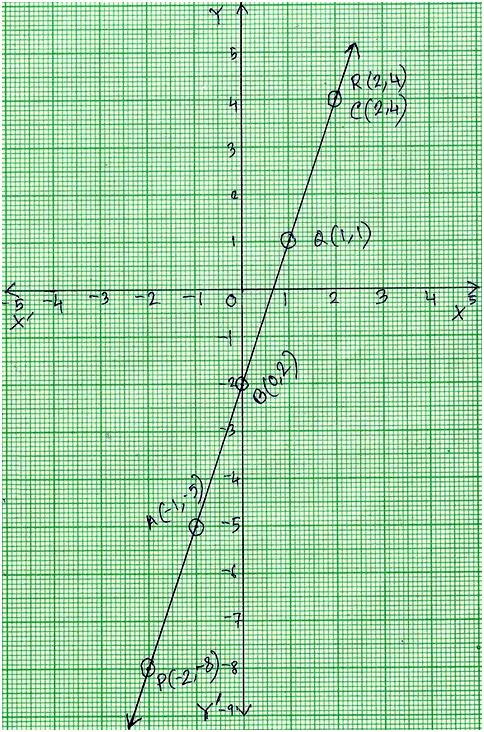


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.