Ordered pair of a Coordinate System

To know the ordered pair of a coordinate system let us recall the coordinate system.

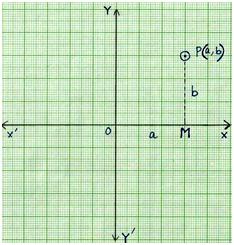
We represent a point in a plane by ordered pairs of real numbers called the Cartesian co-ordinates.  To determine the position of a point in a plane we draw two mutually perpendicular straight lines XOX’ and YOY’.

XOX’ is called the x-axis which is a horizontal line.

YOY’ is called the y-axis which is a vertical line.

Point O is called the origin.

Ordered pair: 

Whenever we write the co-ordinates of a point, first we write the x- co-ordinate, and then we write the y-co-ordinate. Suppose a and b is a pair of two numbers which is listed in a specific order then the co-ordinates (a, b) are called the ordered pair.

Thus, in (a, b) we notice a is at the first place so it is known as x- co-ordinate and b at the second place so it is known as y- co-ordinate. 

In an order pair, if the order of the numbers is changed then it represents a different point,

Hence, (a, b) ≠ (b, a)

Thus, (5, 4) ≠ (4, 5) 

Examples of ordered pair of a coordinate system:

1. In an ordered pair (3, 5): x co-ordinate is 3 and y co-ordinate is 5

But in an ordered pair (5, 3) x co-ordinate is 5 and y co-ordinate is 3

So, we observe that (3, 5) and (5, 3) represent different points.

2. In an ordered pair (7, 2) x co-ordinate is 7 and y co-ordinate is 2

But in an ordered pair (2, 7) x co-ordinate is 2 and y co-ordinate is 7

So, we observe that (7, 2) and (2, 7) represent different points.

Note:

The co-ordinate of the origin are (0, 0) i.e., its x co-ordinate is 0 and its y co-ordinate is also 0.

Related Concepts:

● Coordinate Graph

● Plot Ordered Pairs

● Coordinates of a Point

● All Four Quadrants

● Signs of Coordinates

● Find the Coordinates of a Point

● Coordinates of a Point in a Plane

● Plot Points on Co-ordinate Graph

● Graph of Linear Equation

● Simultaneous Equations Graphically

● Graphs of Simple Function

● Graph of Perimeter vs. Length of the Side of a Square

● Graph of Area vs. Side of a Square

● Graph of Simple Interest vs. Number of Years

● Graph of Distance vs. Time

7th Grade Math Problems

8th Grade Math Practice

From Ordered pair of a Coordinate System to HOME PAGE

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit