Subscribe to our YouTube channel for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Polygon and its Classification
We will learn about polygon and its classification.
A paper represents a plane surface. When we doodle with a pencil on it without lifting out or without using a ruler, some drawings are made which are called curves.
Curves which begin and end at the same point are called closed curves.
Curves which begin and end at the same point but do not cross themselves are called simple closed curves.
Curves which begin and end at different points are called open curves.
Definition of Polygon:
A polygon is a simple closed curve made up of straight line segments only.
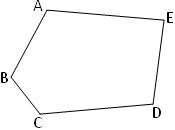
The adjoining figure is a polygon.
(i) closed
(ii) bounded by five line segments AB, BC, CD, DE and AE.
Also, it is clear from the given polygon that:
(i) the five line segments AB, BC, CD, DE and AE intersect at their end points.
(ii) two line segments, with a common vertex, are not collinear i.e. the angle at any vertex is not 180°.
Parts
of a polygon:
(i) Line segments forming a polygon are called sides of the polygon.
(ii) The point where two sides of a polygon meet is called the vertex of the polygon.
(iii) The line segment containing two non-adjacent vertices is called the diagonal of the polygon.
(iv) The angle formed at the vertices inside the closed figure are called interior angles.
Note: The number of sides in a polygon is equal to the number of vertices.
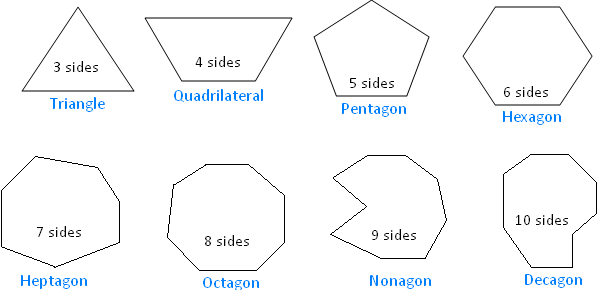
Classification of polygons:
Polygons are classified according to the number of sides or vertices they have.
Diagonal of a polygon:
A line segment connecting any two non-consecutive vertices is called the diagonal of a polygon.
Some examples showing the diagonal of different polygons:
|
In the adjoining figure AC and BD are the two diagonals |
 |
|
In the adjoining figure AD, FC, EB, BF, DB, FD, CA, EC and AE are the nine diagonals. |
 |
The formula for finding the number of diagonals of a polygon is [n(n - 3)]/2, where 'n' is the number of sides.
Note: The polygon triangle has no diagonals.
Some examples showing the sides, vertices and diagonals of different polygons:
|
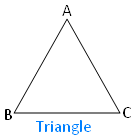
In the adjoining figure AB, BC and CA are the three sides; A, B and C are the three vertices and there is no diagonal. |
 |
|
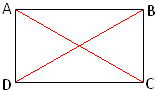
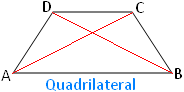
In the adjoining figure AB, BC, CD and DA are the four sides; A, B, C and D are the four vertices and AC and BD are the two diagonals. |
 |
|
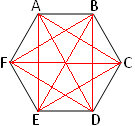
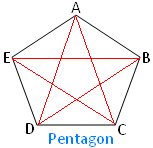
In the adjoining figure AB, BC, CD, DE and EA are the five sides; A, B, C, D and E are the five vertices and AC, BD, EB, DA, and CE are the five diagonals. |
● Polygons
Polygon and its Classification
Interior and Exterior of the Polygon
Number of Triangles Contained in a Polygon
Angle Sum Property of a Polygon
Problems on Angle Sum Property of a Polygon
Sum of the Interior Angles of a Polygon
Sum of the Exterior Angles of a Polygon
7th Grade Math Problems
8th Grade Math Practice
From Polygon and its Classification to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
5th Grade Circle Worksheet | Free Worksheet with Answer |Practice Math
Jul 11, 25 02:14 PM
In 5th Grade Circle Worksheet you will get different types of questions on parts of a circle, relation between radius and diameter, interior of a circle, exterior of a circle and construction of circl… -
Construction of a Circle | Working Rules | Step-by-step Explanation |
Jul 09, 25 01:29 AM
Construction of a Circle when the length of its Radius is given. Working Rules | Step I: Open the compass such that its pointer be put on initial point (i.e. O) of ruler / scale and the pencil-end be… -
Combination of Addition and Subtraction | Mixed Addition & Subtraction
Jul 08, 25 02:32 PM
We will discuss here about the combination of addition and subtraction. The rules which can be used to solve the sums involving addition (+) and subtraction (-) together are: I: First add -
Addition & Subtraction Together |Combination of addition & subtraction
Jul 08, 25 02:23 PM
We will solve the different types of problems involving addition and subtraction together. To show the problem involving both addition and subtraction, we first group all the numbers with ‘+’ and… -
5th Grade Circle | Radius, Interior and Exterior of a Circle|Worksheet
Jul 08, 25 09:55 AM
A circle is the set of all those point in a plane whose distance from a fixed point remains constant. The fixed point is called the centre of the circle and the constant distance is known
● Polygons - Worksheets
Worksheet on Polygon and its Classification
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.