Convex and Concave Polygons

We will learn about the convex and concave polygons and their properties.

Convex polygon:

If each of the interior angles of a polygon is less than 180°, then it is called convex polygon.

Note: In this type of polygon, no portion of the diagonals lies in the exterior.

Examples of convex polygons:

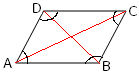
In the adjoining figure of a parallelogram there are four interior angles i.e., ∠BAD, ∠ADC, ∠DCB and ∠CBA. None of the four interior angles is greater than equal to 180° and no portion of the diagonals lies in the exterior.

$Convex Polygon Parallelogram$

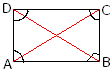
In the adjoining figure of a rectangle there are four interior angles i.e., ∠CBA, ∠DCB, ∠ADC and ∠BAD. None of the four interior angles is greater than equal to 180°.

$Convex Polygon Rectangle$

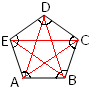
In the adjoining figure of a pentagon there are five interior angles i.e., ∠ABC, ∠BCD, ∠CDE, ∠DEA and ∠EAB. None of the five interior angles is greater than equal to 180°.

$Convex Polygon Pentagon$

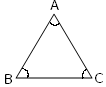
In the adjoining figure of a triangle there are three interior angles i.e., ∠ABC, ∠BCA, and ∠CAB. None of the three interior angles is greater than equal to 180°.

$Convex Polygon Triangle$

Concave polygon:

If at least one angle of a polygon is more than 180°, then it is called a concave polygon.

Examples of concave polygons:

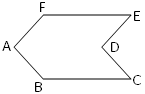
In the adjoining figure of a hexagon there are six interior angles i.e., ∠ABC, ∠BCD, ∠CDE, ∠DEF, ∠EFA and ∠FAB. Among the six interior angles, ∠CDE is greater than 180°.

$Concave Polygon Hexagon$

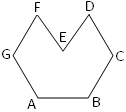
In the adjoining figure of a septagon there are seven interior angles i.e., ∠ABC, ∠BCD, ∠CDE, ∠DEF, ∠EFG, ∠FGA and ∠GAB. Among the seven interior angles, ∠DEF is greater than 180°.

$Concave Polygon Septagon$

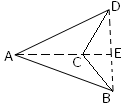
In the adjoining figure of a quadrilateral there are four interior angles i.e., ∠ABC, ∠BCD, ∠CDA and ∠DAB. Among the four interior angles, ∠BCD is greater than 180°.

$Concave Polygon Quadrilateral$