Interior and Exterior of the Polygon
We will learn about the interior and exterior of the polygon.
Interior angles of the polygon:
Two consecutive sides meeting at a common point from an angle called the interior angle of the polygon.
|
A quadrilateral has four interior angles. In the given adjoining figure of a quadrilateral ∠BAD, ∠ADC, ∠DCB and ∠CBA are the four interior angles. |
 |
|
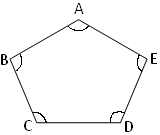
A pentagon has five interior angles. In the given adjoining figure of a pentagon ∠ABC, ∠BCD, ∠CDE, ∠DEA and ∠EAB are the five interior angles. |
 |
|
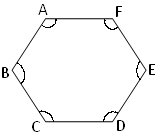
A hexagon has six interior angles. In the given adjoining figure of a hexagon ∠ABC, ∠BCD, ∠CDE, ∠DEF, ∠EFA and ∠FAB are the six interior angles. |
 |
Exterior angles of the polygon:
On extending the side of the polygon, the angle formed outside, between the extended side and its consecutive side is called the exterior angle of the polygon.
|
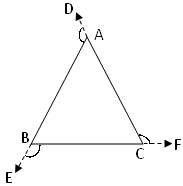
A triangle has three exterior angles. In the given adjoining figure of a triangle ∠BAD, ∠ACF and ∠CBE and are the three exterior angles. |
 |
|
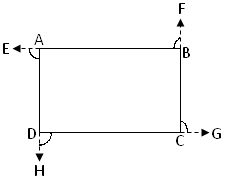
A quadrilateral has four exterior angles. In the given adjoining figure of a quadrilateral ∠DAE, ∠ABF, ∠BCG and ∠CDH are the four exterior angles. |
 |
|
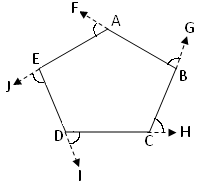
A pentagon has five exterior angles. In the given adjoining figure of a pentagon ∠EAF, ∠ABG, ∠BCH, ∠CDI and ∠DEJ are the five exterior angles. |
 |
Note: An exterior angle and the adjacent interior angle form a linear pair.
`● Polygons
Polygon and its Classification
Interior and Exterior of the Polygon
Number of Triangles Contained in a Polygon
Angle Sum Property of a Polygon
Problems on Angle Sum Property of a Polygon
Sum of the Interior Angles of a Polygon
Sum of the Exterior Angles of a Polygon
7th Grade Math Problems
8th Grade Math Practice
From Interior and Exterior of the Polygon to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
|
|
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.