Patterns in Numbers 

We see so many patterns around us in our daily life. We know that a pattern is an arrangement of objects, colors, or numbers placed in a certain order. Some patterns neither grow nor reduce but only repeat. Such patterns are known as repeating patterns. A pattern has a group of units that follow a rule while repeating or changing. Some examples of patterns are given below:

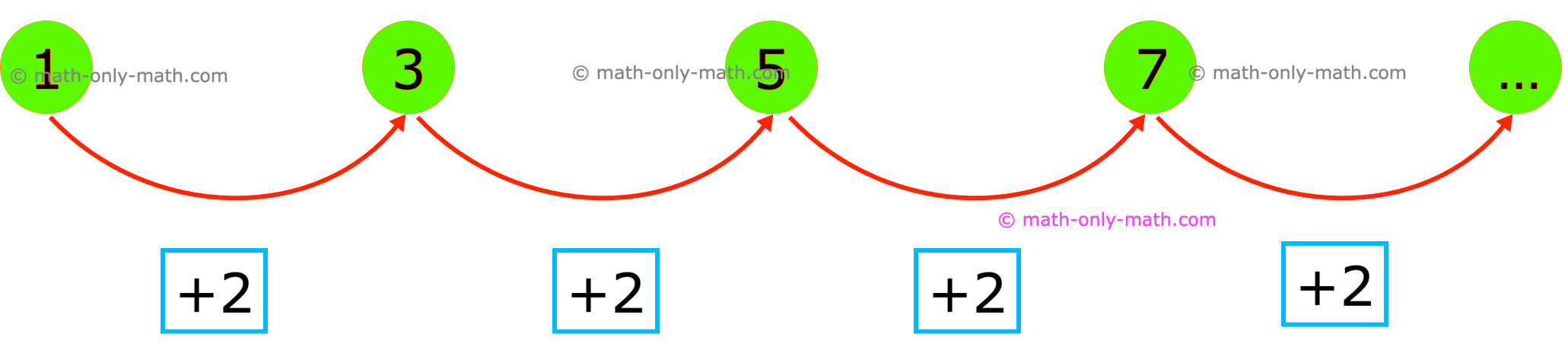
Sometimes sets of numbers have something common in them. They follow a pattern.

Look at the number patterns given below.

Using the numbers, the sequence is:

The rule to go from one number to the next is add 2.

We have to skip count in twos to continue this number sequence.

Patterns in a Number Series

Numbers arranged in a series follow a pattern. If we find the pattern in a series, we can write more numbers in the same series.

1, 3, 5, 7, 9, 11, 一, 一, 一

Here, we see that each number is an odd number and the next number is 2 more than the previous number. So, the next 3 numbers will be 13, 15, and 17.

Patterns in Whole Numbers

Whole numbers can be represented by line segments, triangles, squares, rectangles, etc.

1. Every whole number greater than 1 can be arranged in a line as shown below:

2. Some whole numbers can be represented by triangles. Such numbers are called triangular numbers.

3. Some whole numbers can be represented by squares. These numbers are also known as perfect squares.

4. Some whole numbers can be represented as rectangles.

Let us have a quick review of what we have learnt earlier about patterns.

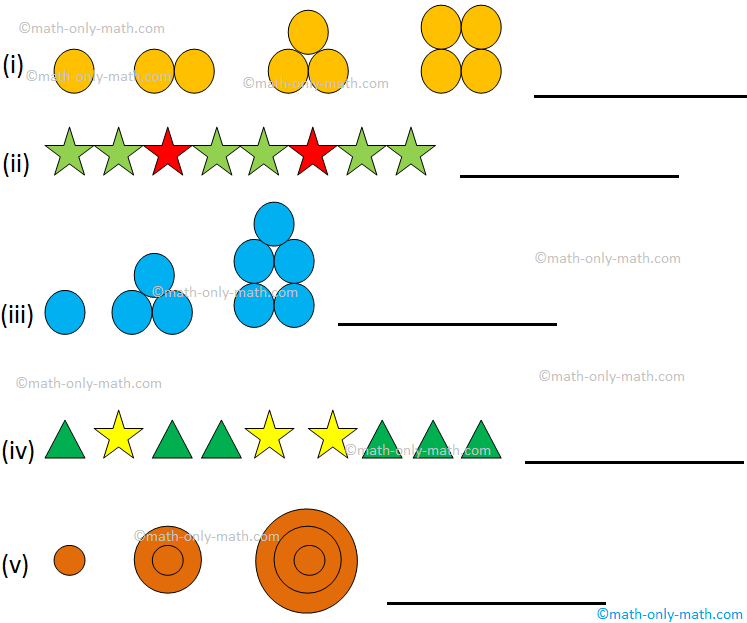
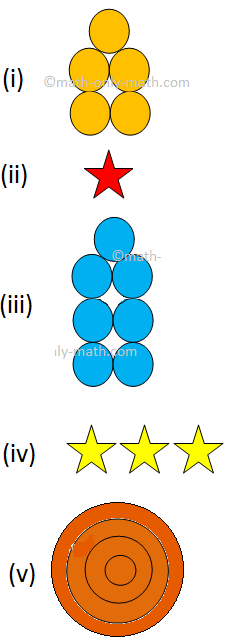
I. Complete the series by drawing the next figure:

Answer:

A pattern can also be created with numbers. The set of numbers which follow a common rule form a pattern. For example, the sequence 2, 4, 6, 8, …… can be extended by using the rule of even numbers. Patterns with numbers can also be created using mathematical operations like addition, subtraction, multiplication and division.

For example:

1. Write the next 3 terms of the pattern 11, 15, 19, 23, ……..

The first term is 11. The common difference is 4. The next 3 terms are 27, 31, 35.

II. Study the patterns in numbers given below :

• 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55

• 11 + 12 + 13 + 14 + 15 + 16 + 17 + 18 + 19 + 20 = 155

• 21 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 30 = 255

Now, complete the following:

(i) 51 + 52 + 53 + 54 + 55 + 56 + 57 + 58 + 59 + 60 = _____

(ii) 61 + 62 + 63 + 64 + 65 + 66 + 67 + 68 + 69 + 70 = _____

(iii) 71 + 72 + 73 + 74 + 75 + 76 + 77 + 78 + 79 + 80 = _____

Answer:

II. (i) 555

(ii) 655

(iii) 755

III. Write the next three terms in each sequence:

(i) 0, 3, 6, 9, ___, ___, ___

(ii) 4, 9, 14, 19, ___, ___, ___

(iii) 10, 15, 20, 25, ___, ___, ___

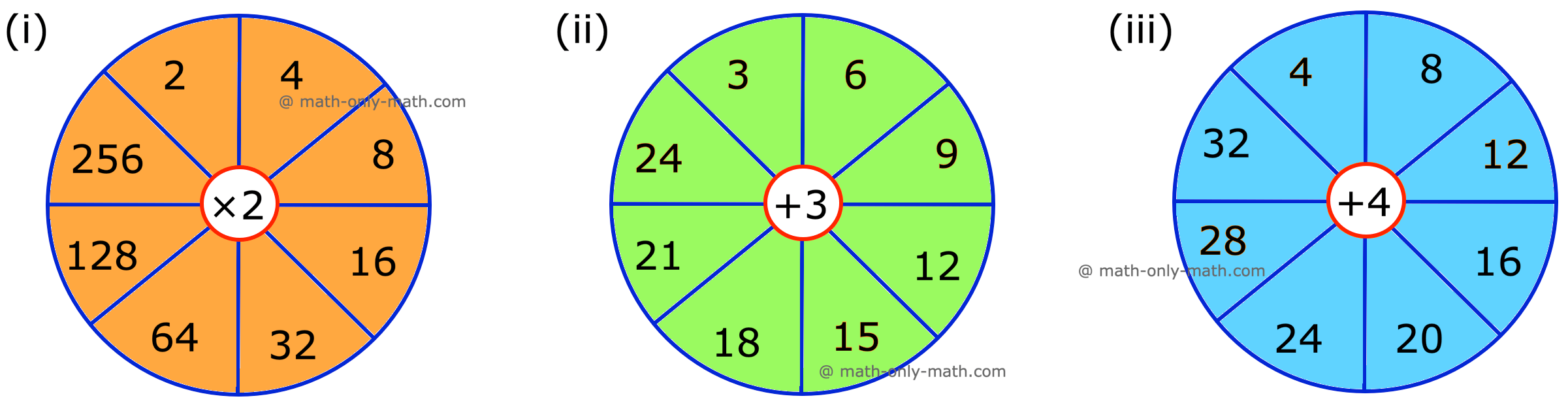
(iv) 2, 4, 8, 16, 32, ___, ___, ___

(v) 98, 87, 76, 65, 54, ___, ___, ___

(vi) 55, 52, 49, 46, 43, ___, ___, ___

Answer:

III. (i) 12, 15, 18

(ii) 24, 29, 34

(iii) 30, 35, 40

(iv) 64, 128, 256

(v) 43, 32, 21

(vi) 40, 37, 34 

Here are some patterns in numbers. Look at them.

• 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

• 1, 1, 2, 2, 3, 3, 4, 4, 5, 5

• 12, 34, 56, 78, 90, 12, 34, 56, 78, 90

• 5, 10, 15, 20, 25, 30, 35, 40, 45, 50

IV. Observe the patterns in numbers and write the next two numbers in the series.

(i) 2, 4, 6, 8, 10, 12, 14, 16, ___, ___

(ii) 1, 3, 5, 7, 9, 11, 13, 15, ___, ___

(iii) 4, 8, 12, 16, 20, 24, 28, 32, ___, ___

(iv) 11, 22, 22, 33, 33, 33, 44, 55, ___, ___

Answer: 

IV. (i) 18, 20

(ii) 17, 19

(iii) 36, 40

(iv) 66, 77

Pattern Observation

The mathematical calculations can be simplified by observing certain patterns.

1. Addition of 9, 99, 999, 9999, etc. to a whole number

For Example:

2. Subtraction of 9, 99, 999, etc. from a whole number.

For Example:

3. Multiplication of a whole number by 9, 99, 999, etc.

For Example:

Here are some patterns in numbers. Follow them and extend them:

(i)

1 × 9 + 2 = 11

12 × 9 + 3 = 111

123 × 9 + 4 = 1111

1234 × 9 + 5 = 11111

12345 × 9 + 6 = _______

123456 × 9 + 7 = _______

(ii)

1 × 8 + 1 = 9

12 × 8 + 2 = 98

123 × 8 + 3 = 987

1234 × 8 + 4 = 9876

12345 × 8 + 5 = _______

123456 × 8 + 6 = _______

(iii)

111 ÷ 3 = 37

222 ÷ 6 = 37

333 ÷ 9 = 37

444 ÷ 12 = 37

         555 ÷ 15 = _______

          666 ÷ 18 = _______

(iv)

      9 + 1 = 10

     90 + 10 = 100

    900 + 100 = 1000

      9000 + 1000 = _______

   90000 + 10000 = _______

900000 + 100000 = _______

Follow the patterns in numbers of the following products and extend them further:

(i)

5 × 5 = 25

55 × 5 = 275

555 × 5 = 2775

5555 × 5 = 27775

_ _ _ _ _ _ _ _ _ _ _ _ _

_ _ _ _ _ _ _ _ _ _ _ _ _

_ _ _ _ _ _ _ _ _ _ _ _ _

55555555 × 5 = 277777775

_ _ _ _ _ _ _ _ _ _ _ _ _

_ _ _ _ _ _ _ _ _ _ _ _ _

_ _ _ _ _ _ _ _ _ _ _ _ _

(ii)

404 × 404 = 163216

505 × 505 = 255025

606 × 606 = 367236

707 × 707 = 499849

808 × 808 = 652864

_ _ _ _ _ _ _ _ _ _ _ _ _

_ _ _ _ _ _ _ _ _ _ _ _ _

_ _ _ _ _ _ _ _ _ _ _ _ _

_ _ _ _ _ _ _ _ _ _ _ _ _

_ _ _ _ _ _ _ _ _ _ _ _ _

_ _ _ _ _ _ _ _ _ _ _ _ _

(iii) Study the following pattern and write the next two steps.

1 × 1 = 1

11 × 11 = 121

111 × 111 = 12321

1111 × 1111 = 1234321

____ × _____ = ________

_____ × _____ = _________

The next two steps will be 

11111 × 11111 = 123454321

111111 × 111111 = 12345654321

SUMMARY:

⚫ Patterns are found in numbers as well.

⚫ When shapes are repeatedly combined, patterns are formed.

⚫ If we find the pattern in a series, we can continue the series.

Worksheet on Patterns in Whole Numbers:

In patterns in numbers here are some unsolved questions for the students to understand and complete the questions on patterns.

I. Complete the given series:

(i) 1, 3, 5, 7, …….., …….., …….., ……..

(ii) 5, 10, 15, 20, …….., …….., …….., ……..

(iii) 10, 20, 30, 40, …….., …….., …….., ……..

(iv) 3, 5, 8, 12, 17, …….., …….., …….., ……..

(v) 10, 20, 35, 55, 80, …….., …….., …….., ……..

(vi) 2, 2, 3, 3, 3, 4, 4, 4, 4, …….., …….., …….., ……..

(vii) 1, 3, 6, 8, 11, 13, 16, …….., …….., …….., ……..

(viii) 35, 45, …….., 65, 75, …….., 95

(ix) 100, 90, 80, …….., 60, 50 ……..

(x) 1, 3, 5, 7, 9, …….., …….., …….., ……..

Answer:

I. (i) 9, 11, 13, 15

(ii) 25, 30, 35, 40

(iii) 50, 60, 70, 80

(iv) 23, 30, 38, 47

(v) 110, 145, 185, 230

(vi) 5, 5, 5, 5, 5

(vii) 18, 21, 23, 26

(viii) 55, 85

(ix) 70, 40

(x) 11, 13, 15, 17

II. Complete the series:

(i) 1, 4, 7, 10, 13, 16, …….., …….., …….., ……..

(ii) 12, 17, 22, 27, 32, …….., …….., …….., ……..

(iii) 6, 16, 26, 36, 46, …….., …….., …….., ……..

(iv) 10, 30, 50, 70, …….., …….., …….., ……..

(v) 38, 35, 32, 29, …….., …….., …….., ……..

(vi) 54, 50, 46, 42, …….., …….., …….., ……..

(vii) 53, 49, 45, 41, …….., …….., …….., ……..

(viii) 23, 30, 37, 44, …….., …….., …….., ……..

Answer:

II. (i) 19, 22, 25, 28

(ii) 137, 42, 47, 52

(iii) 56, 66, 76, 86

(iv) 90, 110, 130, 150

(v) 26, 23, 20, 17

(vi) 38, 34, 30, 26

(vii) 37, 33, 29, 25

(viii) 51, 58, 65, 72

III. Complete the following series:

(i) 7, 14, 21, 28, …….., …….., …….., ……..

(ii) 25, …….., 75, 100, …….., …….., …….., ……..

(iii) 10, 100, …….., 10000, 100000, ……..

(iv) 2, 10, …….., 250, 1250

(v) 500000, 50000, …….., 500, …….., 5

(vi) 64, 32, 16, …….., 4, …….., 1

(vii) 5, 10, 20, …….., 80, …….., 320

(viii) 8, 16, 24, 32, …….., …….., …….., ……..

(ix) 45, 54, 63, …….., …….., …….., ……..

(x) 2, 6, 18, 54, ……..

Answers:

III. (i) 7, 14, 21, 28, …….., …….., …….., ……..

(ii) 25, …….., 75, 100, …….., …….., …….., ……..

(iii) 10, 100, …….., 10000, 100000, ……..

(iv) 2, 10, …….., 250, 1250

(v) 500000, 50000, …….., 500, …….., 5

(vi) 64, 32, 16, …….., 4, …….., 1

(vii) 5, 10, 20, …….., 80, …….., 320

(viii) 8, 16, 24, 32, …….., …….., …….., ……..

(ix) 45, 54, 63, …….., …….., …….., ……..

(x) 2, 6, 18, 54, ……..

IV. Using the shorter method simplify the following.

(i) 226 + 99

(ii) 2157 + 9999

(iii) 1239 + 99999

(iv) 6712 - 999

(v) 42785 - 9999

(vi) 1235 × 999

Answer:

IV. (i) 226 + 99

 = 226 + 100 - 1

= 326 - 1

=  325

(ii) 2157 + 9,999

= 2,157 + 10,000 - 1

= 12,157 - 1

= 12,156

(iii) 1239 + 99999

= 1239 + 100000 - 1

= 101239 - 1

= 101238

(iv) 6712 - 999

= 6712 - (1000 - 1)

= 6712 - 1000 + 1

= 5712 + 1

= 5713

(v) 42785 - 9999

= 42785 - (10,000 - 1)

= 42785 - 10,000 + 1

= 32785 + 1

= 32786

(vi) 1235 × 999

= 1235 × (1000 - 1)

= 123500 - 1235

= 1233765

V. Observe the patterns in numbers and fill in the blanks.

1 × 9 + 1 = 10

12 × 9 + 2 = 110

123 × 9 + 3 = 1110

1234 × 9 + 4 = _____

12345 × 9 + 5 = ______

Answer:

V. 

1234 × 9 + 4 = 11110

12345 × 9 + 5 = 111110

VI. Study the following patterns in numbers and write the next two steps.

1 × 8 + 1 = 9

12 × 8 + 2 = 98

123 × 8 + 3 = 987

1234 × 8 + 4 = 9876

12345 × 8 + 5 = 98765

______ × _ + _ = ______

_______ × __ + __ = _______

Answer:

VI.

123456 × 8 + 6 = 987654

1234567 × 8 + 7 = 9876543

VII. Multiple Choice Questions (MCQ) on Patterns in Numbers:

   Tick (✔) the correct option.

(i) The missing figure in the given pattern is

(ii) Which alphabet complete the series?

A, D, G, J, M ___

(a) N;     (b) O;     (c) P

(iii) The missing number in the given pattern is 5, 12, 19, 26, ___, 40, 47

(a) 29;     (b) 31;     (c) 33

(iv) 8, 12, 16, 20, ___

(a) 24;     (b) 21;     (c) 28

Answer:

VII. (i) → (b)

(ii) → (c) 

(iii) → (c)

(iv) → (a)

VIII. Look for the pattern and write next 3 terms:

(i) 5, 15, 25, 35, ___, ___, ___

(ii) 10, 20, 40, 70, ___, ___, ___

(iii) 1, 4, 7, 10, 13, ___, ___, ___

(iv) 10, 20, 35, 55, ___, ___, ___

Answer:

VIII. (i) 45, 55, 65

(ii) 110, 160, 220

(iii) 16, 19, 22

(iv) 80, 110, 145

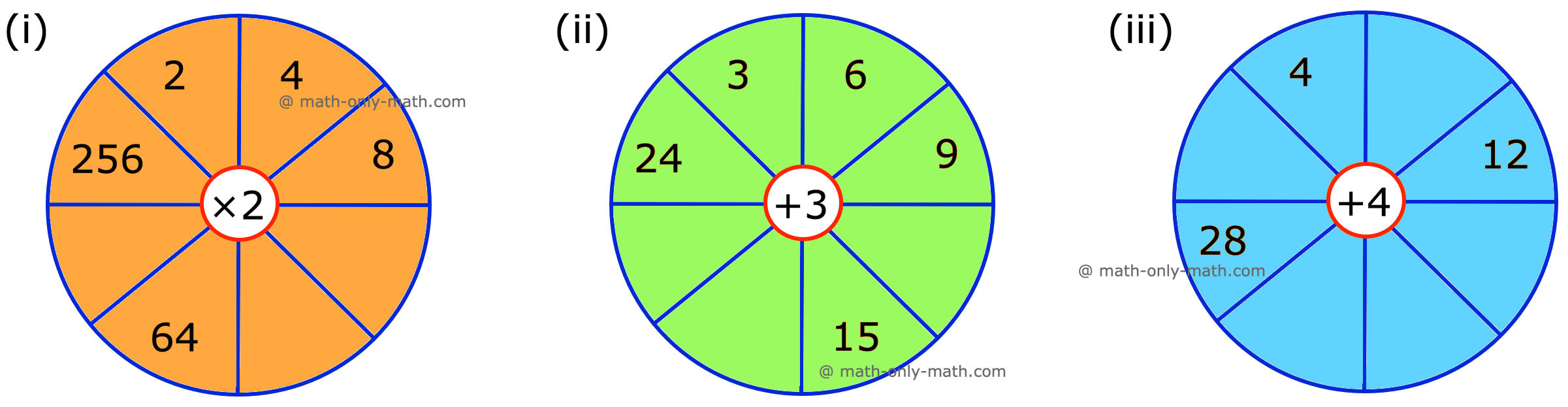
IX. Find the pattern, and fill in the empty spaces in each of the following:

Answer:

IX. 

X. Observe the pattern used in each row and complete the same:

(i) 3, 6, 9, 12, 15, ___, ___, ___, ___, ___, ___.

(ii) 5, 10, 15, 20, 25, ___, ___, ___, ___, ___, ___.

(iii) 4, 8, 12, 16, 20, ___, ___, ___, ___, ___, ___.

(iv) 1, 3, 5, 7, 9, ___, ___, ___, ___, ___, ___.

(v) 80, 75, 70, 65, 60, ___, ___, ___, ___, ___, ___.

Answer:

X. (i) 18, 21, 24, 27, 30, 33

(ii) 30, 35, 40, 45, 50, 55

(iii) 24, 28, 32, 36, 40, 44

(iv) 11, 13, 15, 17, 19, 21

(v) 55, 50, 45, 40, 35, 30

Mental Math Patterns:

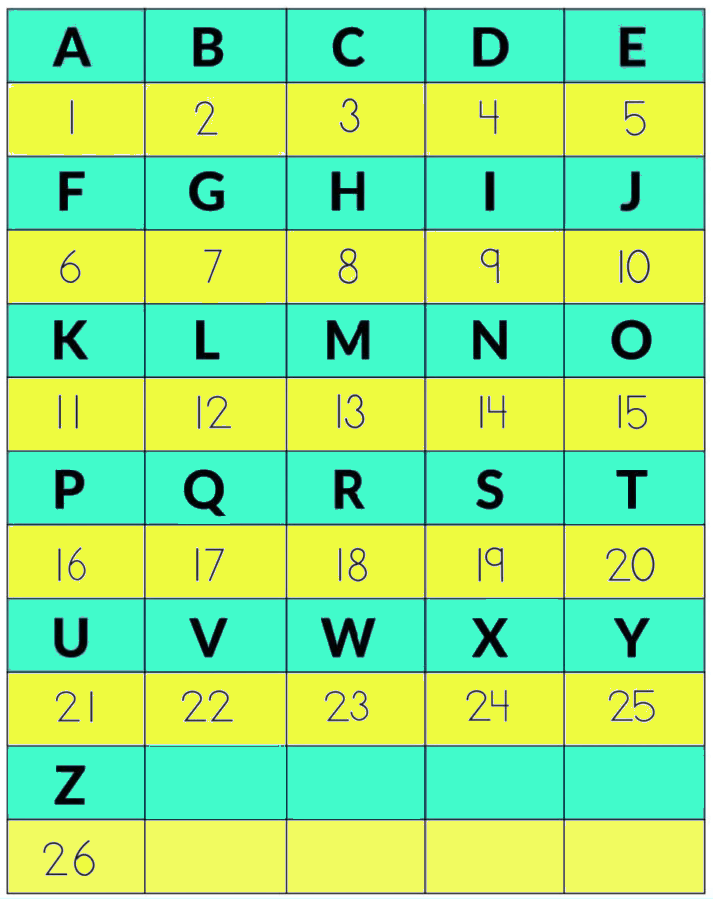
XI. The letters of the alphabet are replaced by numbers 1 to 26 as given in the table.

Decode and write the message:

(i) 19, 8, 21, 20  /  20, 8, 5  /  4, 15, 15, 18

(ii) 12, 5, 20  /  21, 19  /  16,  12, 1, 25

(iii) 9  /  12, 15, 22, 5  /  13, 25  /  9, 14, 4, 9, 1

(iv) 19, 12, 25  /  5, 14, 22, 9, 18, 15, 14, 13, 5, 14, 20

Now play game of coding and decoding messages with your friends.

Answer:

XI. (i) SHUT / THE / DOOR

(ii) LET  /  US  /  PLAY

(iii) I  /  LOVE  /  MY  /  INDIA

(iv) SLY  /  ENVIRONMENT

Related Concept

● Patterns and Mental Mathematics

● Counting Numbers in Proper Pattern

● Odd Numbers Patterns

● Three Consecutive Numbers

● Number Formed by Any Power

● Product of The Number

● Magic Square

● Square of a Number

● Difference of The Squares

● Multiplied by Itself

● Puzzle

● Patterns

● Systems of Numeration

4th Grade Math Activities

From Patterns to HOME PAGE