Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Concept of Pattern
Concept of pattern will help us to learn the basic number patterns and table patterns.
Animals such as all cows, all lions, all dogs and all other animals have dissimilar features. All mangoes have similar features and shapes. Leaves of the same tree have similar pattern of shape. The doors and windows of a house have similar patterns. We may search for similar patterns in mathematics also.
The study of patterns helps students to observe relationships and find continuous connections, to deduce generalizations and predictions.
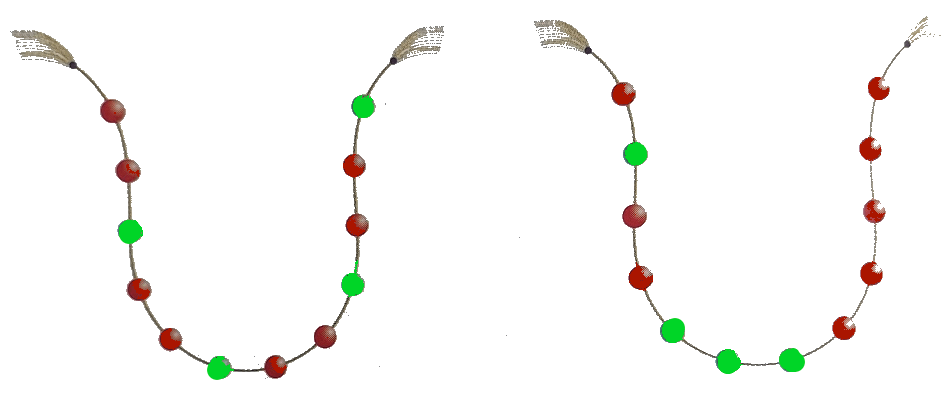
When objects or numbers are placed in some order, a pattern is formed, Look at the necklaces of coloured beads shown below.
Is there any difference in the arrangement of beads in these two necklaces?
In the first necklace, there is a pattern of 2 red beads followed by 1 green bead.
In the second necklace, there is no pattern at all.
There are many patterns around us. A pattern is made when shapes and numbers are repeated or put in a sequence.
We see patterns on cloth, tiles, leaves, flowers, grills in different types of shapes and designs.
Note: A patterns is formed by repeating a senes of objects or sounds.
1. Observe the pattern and tick the one that should come next.
2. Complete the patterns by coloring the shapes.
3. Observe the pattern of numbers and write the ones that should come next.
(i)
2
4
6
8
10
__
__
(ii)
1
2
1
2
1
__
__
4. Observe the pattern and tick the shape that should come next.
Same shapes can be coloured differently to create patterns.
This row of squares has been coloured following the colour code RYGB.
More rows can be added following a similar code. Colour the grid following the colour code given below.
You may have seen such patterns in patchwork quilts.
Observe these patterns in your surroundings.
In everyday life we observe dress pattern, carpet pattern, wall-paper pattern, sari-design pattern as well as number pattern in arithmetic.
Examples of patterns are given below:
2 4 6 8 10 12 …………….;
5 10 15 20 25 30 …………….
The learner has to recognize a pattern and expand it. He must analyze it and then create new patterns to study the subject matter. The teacher should develop in the students the concept of pattern.
(i) To get better idea on the concept of pattern let us look at the following pictures:
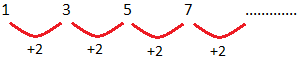
Using the numbers the sequence is:
The rule to go from one number to the next number is ‘add 2’
(ii) In the pattern 1, 3, 5, 7, ……. the number of footballs go on increasing and the number becomes larger each time.
Sometimes the numbers i8n a pattern go on decreasing. Suppose there are 16 footballs in the basket. A person gives two footballs to each group of players for the football match. The number of footballs in the basket goes on decreasing by each group.
The pattern is:
The missing numbers are 8, 6 and 4. The rule of the pattern is to take away 2 each time.
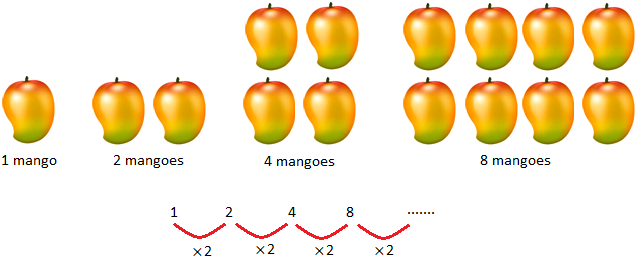
(iii) The numbers becomes larger and larger very rapidly.
The missing number is 16. The rule to go from one term to the next is multiply by 2.
Here are some examples of designs having the same pattern:
Number Patterns / Patterns in Numbers:
Observe the pattern of numbers and write the one that should come next.
(a) 1, 2, 3, 4, 5, _____
(b) 9, 8, 7, 6, 5, _____
(c) 4, 8, 12, 16, _____
(d) 11, 22, 33, 44, 55, _____
A pattern may also be created by repeated numbers. To understand the order, we have to find out the order in which the numbers have been arranged.
|
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
0 |
1 |
2 |
Here, we can see three digits 0, 1, and 2 being repeated in the same order.
|
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
Here, we see the digit 1 being written after 1 and the 2 being written after 2. This set of four is being repeated.
|
1 |
2 |
3 |
3 |
2 |
1 |
1 |
2 |
3 |
3 |
2 |
1 |
Here, we see the digits increasing from 1 to 3 and then decreasing from 3 to 1. This set of six is being repeated.
Different Types of Numbers of Patterns:
1 + 2 + 3 + 4 + 5 + ……. + 10 = 55
Sum of the numbers from 1 to 10 is 55
Hence, the sum of the numbers from 11 to 20 will be 10 × 10 = 100 more than 55
11 + 12 + 12 + ……. + 20 = 155
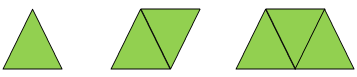
Look at the following pattern that grows when you add triangles.
The pattern can be represented in numbers as 1, 2, 3.
A pattern like given above will form a sequence 1, 4, 9, 16, 25, …..
Table Patterns:
(i) 2, 4, 6, 8, 10, …….
In table 2, we see every forward number is 2 more than its previous one.
(ii) 2, 8, 14, 20, 26, …….
Every forward number is 6 more than the previous one.
|
(iii) 1 + 2 + 3 + 4 + 5 = 15 |
Sum of first 5 consecutive numbers = 15 |
|
2 + 3 + 4 + 5 + 6 = 20 |
Sum of 2 to 6 consecutive numbers = 15 + 5 = 20 |
|
3 + 4 + 5 + 6 + 7 = 25 |
Sum of 3 to 6 consecutive numbers = 15 + 2 × 5 = 25 |
|
11 + 12 + 13 + 14 + 15 = 65 |
Sum of 11 to 15 consecutive numbers = 15 + (11 - 1) × 5 = 15 + (10 × 5) = 15 + 50 = 65 |
Questions and Answers on Concept of Pattern:
I. Observe the rule and write the next number in the series.
(i) 5, 10, 15, 20, ........, ........, ........, ........, ........, ........
(ii) 1, 2, 3, ........, ........, ........, ........, ........, ........, ........
(iii) 10, 20, ........, ........, ........, ........, ........, ........, ........, ........
(iv) 10, 9, 8, ........, ........, ........, ........, ........, ........, ........
Answer:
I. (i) 25, 30, 35, 40, 45, 50
(ii) 4, 5, 6, 7, 8, 9, 10
(iii) 30, 40, 50, 60, 70, 80, 90, 100
(iv) 7, 6, 5, 4, 3, 2, 1
A number sequence follows a pattern. We can make number patterns by applying a rule.
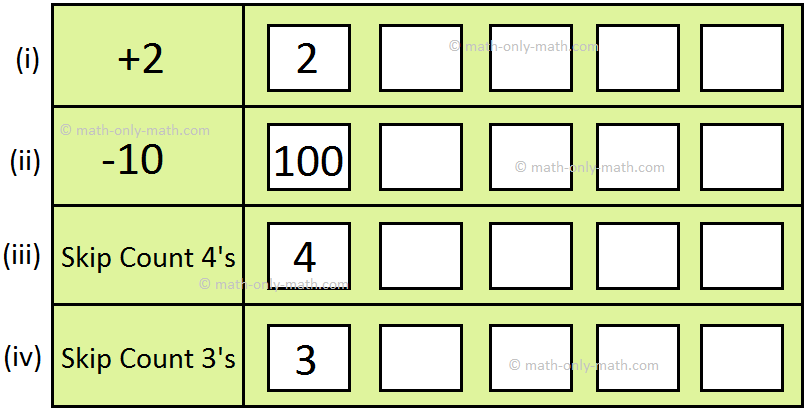
II. Make a number sequence by applying the given rule.
Answer:
II. (i) 4, 6, 8, 10
(ii) 90, 80, 70, 60
(iii) 8, 12, 16, 20
(iv) 6, 9, 12, 15
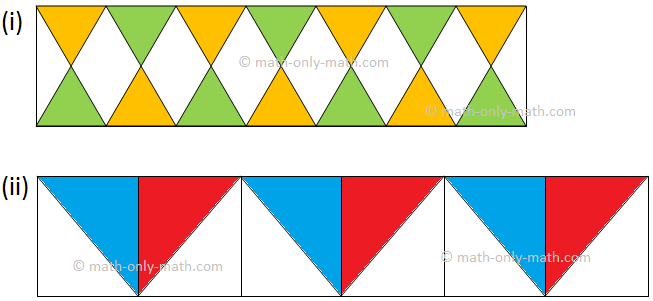
III. Complete the given pattern. One is done for you.
Answer:
III.
IV. Draw a zebra crossing pattern in the following space.
Answer:
IV.
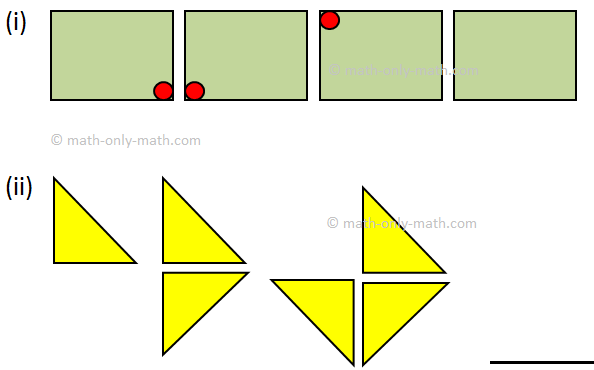
V. Continue the pattern.
Answer:
V.
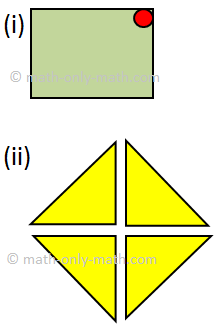
VI. Complete the pattern and color.
Answer:
VI.
VII. Find the rule used in this number pattern.
(i) 55, 45, 35, 25, ... _______________
(ii) 36, 39, 42, ... _______________
(iii) 50, 45, 40, 35, ... _______________
(iv) 10, 20, 30, 40, ... _______________
Answer:
VII.
(i) -10
(ii) +3
(iii) -5
(iv) +10
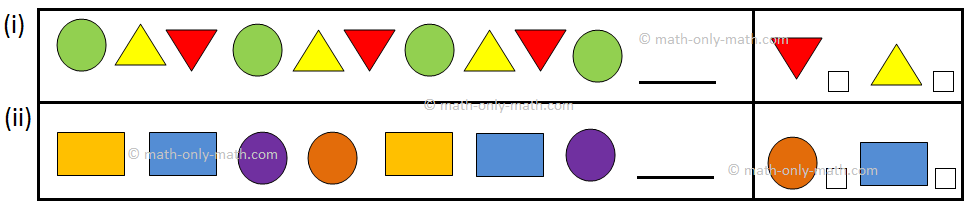
VIII. Tick the shape that comes next.
Answer:
VIII.
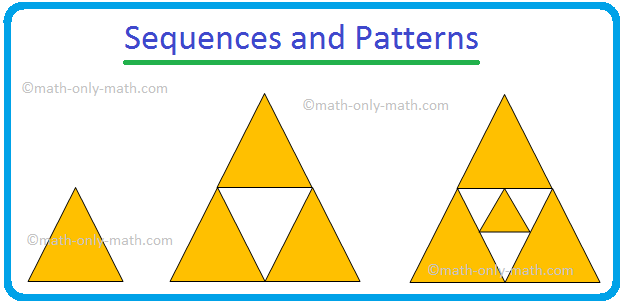
IX. Look at the picture and write the answers.
(i) What shape is used in this pattern?
(ii) How many times is the shape used?
(iii) How many white square boxes are there?
(iv) How many black square boxes are there?
(v) Do you see any number pattern?
Answer:
IX.
(i) Square
(ii) 64
(iii) 32
(iv) 32
X. Complete and color the pattern.
Answer:
X.
IX. Draw the next pattern in the given picture.
Answer:
IX.
X. Observe the rule and write what comes next.
(i) 110, 120, 130, _____, _____, _____, _____, _____.
(ii) 2, 4, 6, _____, _____, _____, _____, _____.
(iii) 90, 89, 88, _____, _____, _____, _____, _____.
(iv) 16, 20, 24, _____, _____, _____, _____, _____.
Answer:
X. (i) 140, 150, 160, 170, 180.
(ii) 8, 10, 12, 14, 16.
(iii) 87, 86, 85, 84, 83.
(iv) 28, 32, 36, 40, 44.
XI. Look for a pattern and fill in the missing numbers.
Answer:
XI. (i) 11, 13
(ii) 18, 21
(iii) 50, 40
(iv) 500, 600
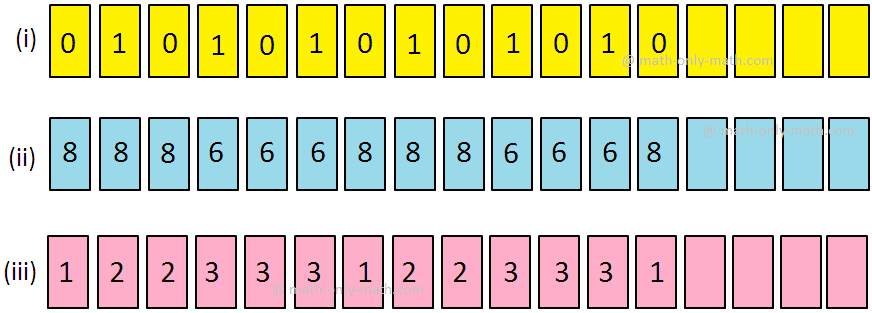
XII. Observe the pattern of numbers and fill in the blanks to complete the series.
Answer:
XII. (i) 1, 0, 1, 0
(ii) 8, 8, 6, 6
(iii) 2, 2, 3, 3
XII. Observe the number pattern and write what should come next.
(i) 1, 22, 333, 4444, 55555, ______
(ii) 1, 2, 2, 3, 4, 4, 5, 6, 6, ______
(iii) 1, 1, 2, 3, 3, 4, 5, 5, 6, ______
(iv) 3, 13, 23, 33, 43, ______
Answer:
XII. (i) 666666
(ii) 7
(iii) 7
(iv) 53
From Concept of Pattern to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.









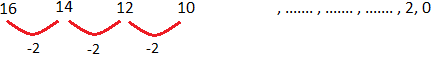
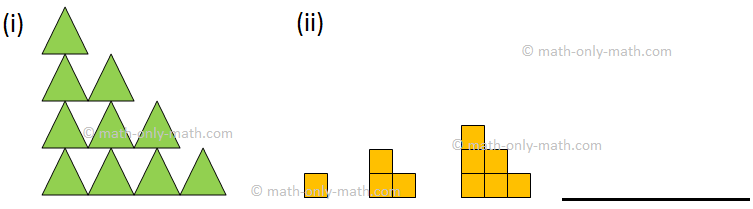
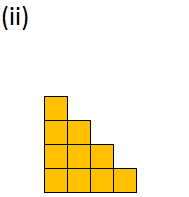

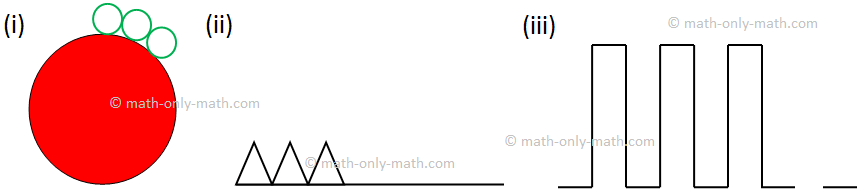
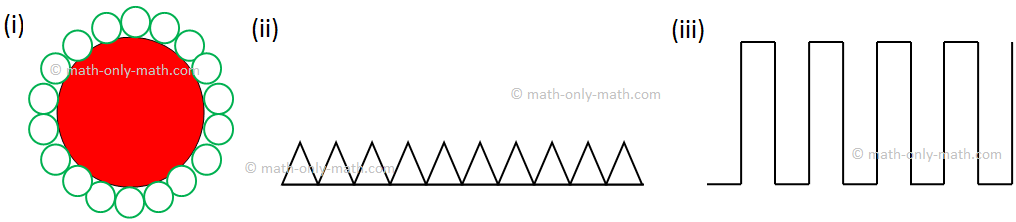





New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.