Systems of Numeration

We know two systems of numeration.

(i) Hindu-Arab System of numbers based on 10 digits, i.e., 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.

(ii) Roman System of numbers based on 5 digits, i.e., I, V, X, L, C, D and M.

The numbers based on 10 digits and 5 digits may be interchanged.

(iii) There is a third system of numbers named as computer system. This system of numbers is based on two digits, i.e., 0 and 1.

This system is also called 2-digit based number system.

The numerals of numbers in the three systems are as follows.

10-digit-based numbers: 358293, 934528

5-digit-based numbers: XL, CDXXVI, MMC

2-digit-based numbers: 1101011, 1101111

The two-digit based numbers and 10-digit based numbers may be interchanged.

In 10-digit based numbers, the place values from right to left are as follows:

In 2-digit based numbers, the place values from right to left are given below.

Let there be a 2-based number (1101011)₂ and we have to write it as a 10-based number:

The 2-based number is written in its extended form (i.e., according to the place value) as shown here:

Therefore, Number = 64 + 32 + 0 + 8 + 0 + 2 + 1 = 107= (2-based number) 1101011 = (10-based number) 107

In short 2-based number 1101011 may be changed into 10-based number

Therefore, Number = 64 + 32 + 0 + 8 + 0 + 2 + 1 = 107 = (2-based number) 1101011 = (10-based number) 107

In short 2-based number 1101011 may be changed into 10-based number

(1101011)₂ = 1 x 2⁶ + 1 x 2⁵ + 0 x 2⁴ + 1 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2⁰

          = (1 x 64) + (1 x 32) + (0 x 16) + (1 x 8) + (0 x 4) + (1 x 2) + (1 x 1)

          = 64 + 32 + 0 + 8 + 0 + 2 + 1

          = (107)₁₀

The 10-based number may also be changed into 2-based number.



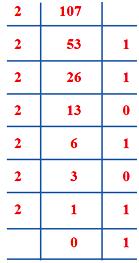
Say, we have to change (107)₁₀ into 2-based number.



2-based number = 11010111

(i) 107 is divided by 2, quotient is 53 the remainder is 1.
This remainder 1 is the digit of 2-based number having place 2⁰ = 1

(ii) 53 is divided by 2, quotient is 26 the remainder is 1, it is the digit of 2-based number having place value 2¹ = 2

(iii) 26 is divided by 2, quotient = 13, R = 0.
Remainder 0 has the place value 2² = 4 where 0 x 4 = 0

(iv) 13 is divided by 2, quotient = 6, R = 1, place value = 2³ = 8, 1 x 8 = 8

(v) 6 is divided by 2, Quotient = 3, R = 0, place value of 0 = 24, 0 x 16 = 0

(vi) 3 is divided by 2, quotient = 1, R = 1, place value of 1 x 2⁵ = 1 x 32 = 32

(vii) 1 is divided by 2, quotient = 0, R = 1,place value = 1 x 2⁶ = 1 x 64 = 64

Therefore, (107)₁₀ = (1101011)₂

2-based number = 1101011

10-based number = 64 + 32 + 0 + 8 + 0 + 2 + 1 = (107)₁₀

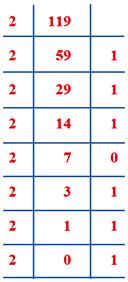
Say we have to change (119)₁₀ into 2-based number.

Verification

    1     1     1     0     1     1     1

= 2⁶ + 2⁵ + 2⁴ + 2³ + 2² + 2¹ + 2⁰

= 64 + 32 + 16 + 0 + 4 + 2 + 1

= 119

Related Concept

● Patterns and Mental Mathematics

● Counting Numbers in Proper Pattern

● Odd Numbers Patterns

● Three Consecutive Numbers

● Number Formed by Any Power

● Product of The Number

● Magic Square

● Square of a Number

● Difference of The Squares

● Multiplied by Itself

● Puzzle

● Patterns

4th Grade Math Activities

From Systems of Numeration to HOME PAGE