Parallelogram

In a parallelogram; opposite sides are equal, opposite angles are equal and diagonals bisect each other.

Prove that in a parallelogram: 

(i) the opposite sides are equal; 

(ii) the opposite angles are equal; 

(iii) diagonals bisect each other. 

Proof:

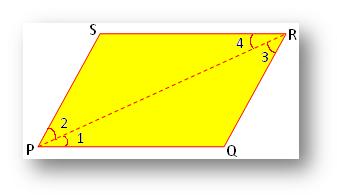
Let PQRS be a parallelogram. Draw its diagonal PR.

In ∆ PQR and ∆ RSP,

∠1 = ∠4       (alternate angles) 

∠3 = ∠2       (alternate angles) 

and PR = RP  (common) 

Therefore, ∆ PQR ≅ ∆ RSP (by ASA congruence) 

⇒ PQ = RS, QR = SP and ∠Q = ∠S. 

Similarly, by drawing the diagonal QS, we can prove that 

∆ PQS ≅ ∆ RSQ

Therefore, ∠P = ∠R

Thus, PQ = RS, QR = SP, ∠Q = ∠S and ∠P = ∠R. 

This proves (i) and (ii) 

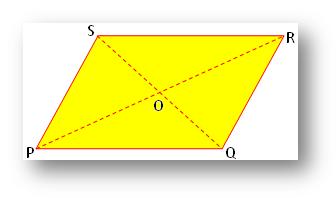
In order to prove (iii) consider parallelogram PQRS and draw its diagonals PR and QS, intersecting each other at O.

In ∆ OPQand ∆ ORS, we have

PQ = RS                            [Opposite sides of a parallelogram]

∠POQ = ∠ ROS                   [Vertically opposite angles]

∠OPQ = ∠ORS                    [Alternate angles]

Therefore, ∆ OPQ ≅ ∆ ORS   [By ASA property]

⇒ OP = OR and OQ = OS.

This shows that the diagonals of a parallelogram bisect each other.

The converse of the above result is also true, i.e.,

(i) If the opposite sides of a quadrilateral are equal then it is a parallelogram.

(i) If the opposite angles of a quadrilateral are equal then it is a parallelogram.

(i) If the diagonals of a quadrilateral bisect each other then it is a parallelogram.

Parallelogram

Parallelogram

Properties of a Rectangle Rhombus and Square

Problems on Parallelogram

Practice Test on Parallelogram

Parallelogram - Worksheet

Worksheet on Parallelogram

8th Grade Math Practice

From Parallelogram to HOME PAGE