Worksheet on Parallelogram
In the worksheet on parallelogram students can practice 14 different types of problems.
1. ABCD is a parallelogram in which ∠A = 110°. Find the measure of each of the angles ∠B, ∠C and ∠D.
2. Two adjacent angles of a parallelogram are equal. What is the measure of each of these angles?
3. Two adjacent angles of a parallelogram are in the ratio 4 : 5. Find the measure of each of its angles.
4. Two adjacent angles of a parallelogram are (3x - 4)° and (3x + 16)°. Find the value of x and hence find the measure of each of its angles.
5. The sum of two opposite angles of a parallelogram is 130°. Find the measure of each of its angles.
6. Two sides of a parallelogram are in the ratio 5 : 3. If its perimeter is 64 cm, find the lengths of its sides.
7. The perimeter of a parallelogram is 140 cm. If one of the sides is longer than the other by 10 cm, find the length of each of its sides.
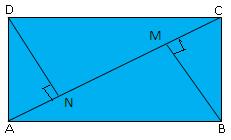
8. In the adjacent figure, ABCD is a rectangle. If BM and DN are perpendiculars from B and D on AC, prove that ∆ BMC ≅ ∆ DNA. Is it true that BM = DN?
Hint: In triangles BMC and DNA,
BC = DA, ∠BCM = ∠DAN (alternate angles) and ∠DNA = ∠BMC = 90°
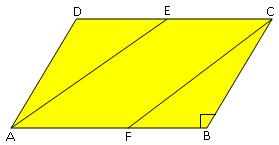
9. In the adjacent figure, ABCD is a parallelogram and line segments AE and CF bisect the angles A and C respectively. Show that AE ∥ CF.
Hint: In triangles ADE and CBF, we have AD = BC, ∠B = ∠D
and ∠DAE = ∠BCF.
[Since, ∠A = ∠C = ¹/₂∠A = ¹/₂∠C, ie., ∠DAE = ∠BCF]
Therefore, ∆ ADE ≅ ∆CBF. And therefore, CD - DE = AB - BF.
So, CE = AF.
Therefore, AECF is a parallelogram.
Hence, AE ∥ CF.
10. The lengths of the diagonals of a rhombus are 16 cm and 12 cm respectively. Find the length of each of its sides.
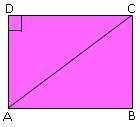
11. In the given figure ABCD is a square. Find the measure of ∠CAD.
Hint: DA = DC ⇒ ∠ACD = ∠DAC = x° (say) Then, x° + x° + 90° = 180°. Find x.
12. The sides of a rectangle are in the ratio 5 : 4 and its perimeter is 90 cm. Find its length and breadth.
13. Name each of the following parallelograms.
(i) The diagonals are equal and the adjacent sides are unequal.
(ii) The diagonals are equal and the adjacent sides are equal.
(iii) The diagonals are unequal and the adjacent sides are equal.
(iv) All the sides are equal and one angle is 60°.
(v) All the sides are equal and one angle is 90°.
(vi) All the angles are equal and the adjacent sides are unequal.
14. Which of the following statements are true or false?
(i) The diagonals of a parallelogram are equal.
(ii) The diagonals of a rectangle are perpendicular to each other.
(iii) The diagonals of a rhombus are equal.
(iv) Every rhombus is a kite.
(v) Every rectangle is a square.
(vi) Every square is a parallelogram.
(vii) Every square is a rhombus.
(viii) Every rectangle is a parallelogram.
(ix) Every parallelogram is a rectangle.
(x) Every rhombus is a parallelogram.
Answers for worksheet on parallelogram are given below so that students can check the answers after solving the questions on parallelogram to make sure that the answer is correct.
Answers:
1. ∠B = 70°, ∠C = 110°, ∠D =70°
2. 90°
3. 80°, 100°, 80°, 100°
4. x = 28, 80°, 100°, 80°, 100°
5. 65°, 115°, 65°, 115°
6. 20 cm, 12 cm
7. 40 cm, 30 cm
8. Yes
9. 10 cm
11. 45°
12. length = 25 cm, breadth = 20 cm
13. (i) rectangle
(ii) square
(iii) rhombus
(iv) rhombus
(v) square
(vi) rectangle
14. (i) False
(ii) False
(iii) False
(iv) False
(v) False
(vi) True
(vii) True
(viii) True
(ix) False
(x) True
Parallelogram
Properties of a Rectangle Rhombus and Square
Practice Test on Parallelogram
Parallelogram - Worksheet
8th Grade Math Practice
From Worksheet on Parallelogram to HOME PAGE
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.