Subscribe to our YouTube channel for the latest videos, updates, and tips.
Figure on Same Base and between Same Parallels
Here we will learn about the
figure on same base and between same parallels. We know the measure of the
plane region enclose by a closed figure is called its area.
Two geometric figures are said to be on the same base and between the same parallels, if they have a common side as base and vertices opposite to the common base lie on the line parallel to the base.
|
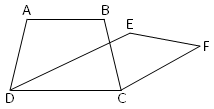
Trapezium ABCD and parallelogram EFCD have a common side DC. We say that trapezium ABCD and parallelogram EFCD are on the same base DC. |
|
Parallelograms ABCD and EFCD are on the same base DC. | |
|
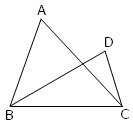
Triangles ABC and DBC are on the same base BC. |
 |
|
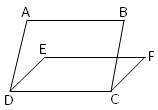
Parallelograms ABCD and triangle EFCD are on the same base DC. |
Solved example for the figure on same base and between same parallels:
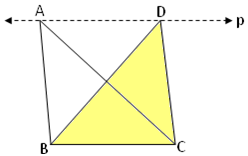
1. Here ∆ABC and ∆DBC have the same base BC and are between the same parallel ‘p’ and BC.
Base and altitude of the figure
Base: Any side of the figure is called the base.
Altitude: A line segment joining the vertex and perpendicular to the opposite side is called the altitude.
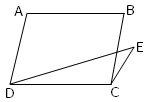
2. ABC is right angled at B with BC = 6 cm and AC = 10 cm. also ∆ABC and ∆BCD are on the same base BC. Find the area of ∆BCD.
Solution:
In right angled ∆ ABC, AC = 10 cm and BC = 6 cm. using Pythagoras theorem, we get
AC2 = AB2 + BC2102 = x2 + 62
⇒ x2 = 102 – 62
⇒ x2 = 100 – 36
⇒ x2 = 64
⇒ x = √64
⇒ x = √(8 × 8)
⇒ x = 8 cm
Now, since ∆ ABC and ∆BCD are on the same base BC.
Therefore, area of ∆ ABC = Area of ∆BCD
⇒ 1/2 × base × height = Area of ∆BCD
⇒ 1/2 × 6 × 8 = Area of ∆BCD
Therefore, area of ∆BCD = 6 × 4 cm2= 24 cm2
Figure on Same Base and between Same Parallels
Parallelograms on Same Base and between Same Parallels
Parallelograms and Rectangles on Same Base and between Same Parallels
Triangle and Parallelogram on Same Base and between Same Parallels
Triangle on Same Base and between Same Parallels
8th Grade Math Practice
From Figure on Same Base and between Same Parallels to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
8 Times Table | Multiplication Table of 8 | Read Eight Times Table
May 18, 25 04:33 PM
In 8 times table we will memorize the multiplication table. Printable multiplication table is also available for the homeschoolers. 8 × 0 = 0 8 × 1 = 8 8 × 2 = 16 8 × 3 = 24 8 × 4 = 32 8 × 5 = 40 -
Worksheet on Average | Word Problem on Average | Questions on Average
May 17, 25 05:37 PM
In worksheet on average interest we will solve 10 different types of question. Find the average of first 10 prime numbers. The average height of a family of five is 150 cm. If the heights of 4 family -
How to Find the Average in Math? | What Does Average Mean? |Definition
May 17, 25 04:04 PM
Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities. -
Problems Based on Average | Word Problems |Calculating Arithmetic Mean
May 17, 25 03:47 PM
Here we will learn to solve the three important types of word problems based on average. The questions are mainly based on average or mean, weighted average and average speed. -
Rounding Decimals | How to Round a Decimal? | Rounding off Decimal
May 16, 25 11:13 AM
Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.