Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Parallelograms and Rectangles on Same Base and between Same Parallels
Parallelograms and rectangles on same base and between same parallels are equal in area.
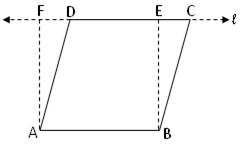
In the adjoining figure, parallelogram ABCD and rectangle ABEF are on the same base BC and between the same parallels AB and l.
Therefore, area of parallelogram ABCD = Area of rectangle ABEF
= AB × AF
AF is also the altitude of the parallelogram.
Hence, area of the parallelogram = base × height
= AB × AF
Solved examples for the rectangles and parallelograms on same base and between same parallels:
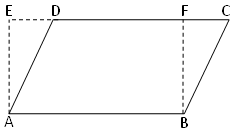
1. Parallelogram ABCD and rectangle ABFE have some base AB, and the length and breadth of the rectangle are as 7 cm and 4 cm. find the area of the parallelogram.
Solution:
Length of rectangle = 7 cm
Breadth of rectangle = 4 cm
Therefore, area of rectangle = 7 × 4 cm2= 28 cm2
Since, rectangle ABFE and parallelogram ABCD are on the same base AB.
Therefore, area of parallelogram = Area of rectangle
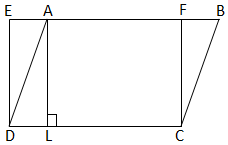
Therefore, area of parallelogram ABCD = 28 cm22. In the adjacent figure ABCD is a parallelogram and EFCD is a rectangle.
Also, AL ⊥ DC. Prove that
(a) Area (ABCD) = Area (EFCD)
(b) Area (ABCD) = DC × AL
Solution:
(a) As a rectangle is also a parallelogram,
Therefore, Area (ABCD) = Area (EFCD)
(b) From above result,
Area (ABCD) = DC × FC (Area of the rectangle = length × breadth) ……………… (i)
As AL ⊥ DC, therefore, AFCL is also a rectangle
So, AL ⊥ FC ……………… (ii)
Therefore, from (i) and (ii) we get
Area (ABCD) = DC × AL
From the above result we see that, area of a parallelogram is the product of it’s any side and the corresponding altitude.
Figure on Same Base and between Same Parallels
Parallelograms on Same Base and between Same Parallels
Parallelograms and Rectangles on Same Base and between Same Parallels
Triangle and Parallelogram on Same Base and between Same Parallels
Triangle on Same Base and between Same Parallels
8th Grade Math Practice
From Parallelograms and Rectangles on Same Base and between Same Parallels to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Area, Perimeter and Volume | Square, Rectangle, Cube,Cubo
Jul 25, 25 12:21 PM
In this worksheet on area perimeter and volume you will get different types of questions on find the perimeter of a rectangle, find the perimeter of a square, find the area of a rectangle, find the ar… -
Worksheet on Volume of a Cube and Cuboid |The Volume of a RectangleBox
Jul 25, 25 03:15 AM
We will practice the questions given in the worksheet on volume of a cube and cuboid. We know the volume of an object is the amount of space occupied by the object.1. Fill in the blanks: -
Volume of a Cuboid | Volume of Cuboid Formula | How to Find the Volume
Jul 24, 25 03:46 PM
Cuboid is a solid box whose every surface is a rectangle of same area or different areas. A cuboid will have a length, breadth and height. Hence we can conclude that volume is 3 dimensional. To measur… -
Volume of a Cube | How to Calculate the Volume of a Cube? | Examples
Jul 23, 25 11:37 AM
A cube is a solid box whose every surface is a square of same area. Take an empty box with open top in the shape of a cube whose each edge is 2 cm. Now fit cubes of edges 1 cm in it. From the figure i… -
5th Grade Volume | Units of Volume | Measurement of Volume|Cubic Units
Jul 20, 25 10:22 AM
Volume is the amount of space enclosed by an object or shape, how much 3-dimensional space (length, height, and width) it occupies. A flat shape like triangle, square and rectangle occupies surface on…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.