Subscribe to our YouTube channel for the latest videos, updates, and tips.
Worksheet on Same Base and Same Parallels
Worksheet on same base and same parallels will help us to practice the different types of questions on area proportions.
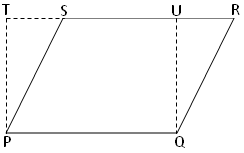
1. Parallelogram PQRS and rectangle PQUT are on the same base PQ and between the same parallels PQ and TR. Also, the area of the parallelogram is 63 cm^2 and the width of the rectangle is 9 cm. Find the length of the rectangle and its area.
2. In the adjoining figure, ∆PQR is right angled at Q in which QR = 6 cm and PQ = 7 cm. Find the area of ∆QSR; given that PS∥QR.
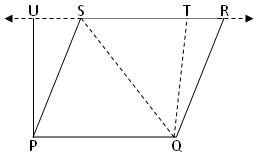
3. Parallelogram PQRS and PQTU are on the same base PQ and between same parallels PQ and UR. Area of parallelogram PQRS = 56 cm^2 and the altitude of the parallelogram PQTU = 7 cm. Find the length of the common side of two parallelograms.
4. Parallelogram PQRS, ∆PQS, and rectangle PQTU have the same base PQ. If the area of ∆PSQ = 48 cm^2, then find the area of parallelogram PQRS and the area of rectangle PQTU.
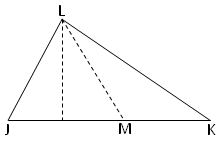
5. LM is median of ∆JKL, JK = 10 cm and the altitude of the ∆JKL = 4 cm, find the area of ∆JLM and area of ∆LMK
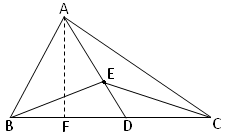
6. AD is the median of ∆ABC. E is any point on AD. Show that area of ∆ABE = area of ∆ACE
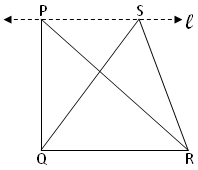
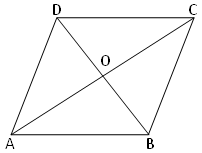
7. The diagonal of the quadrilateral ABCD, (DB, AC) intersect at O. If OB = OD, then show that ∆ABC and ∆ADC have same areas.
[Hint: AO is the median of ∆ADB. Find area of triangles AOD and AOB …………… (1)
OC is the median ∆DCB. Find areas of triangles DOC and BOC …………… (2)
Add (1) and (2)].
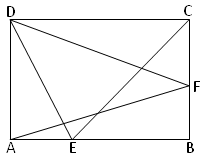
8. In the parallelogram ABCD, E, F are any two points on sides AB and BC respectively. Show that ∆DFA and ∆DEC have same areas.
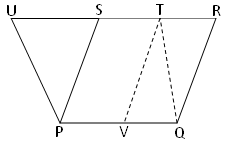
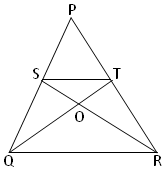
9. ∆PQR is isosceles triangle with ST//QR. The medians SR and QT intersect each other at O.
Prove that area of (1) ∆QTS = ∆RST
(2) ∆QOS = ∆ROT
(3) ∆PQT = ∆PRS
Answers for the worksheet on same base and same parallels are given below to check the exact answer.
Answers:
1. Length = 7 cm, Area = 63 cm^2
2. Area = 21 cm^2
3. Length = 8 cm
4. Area = 96 cm^2
5. Area = 10 cm^2
Math Home Work Sheets
From Worksheet on Same Base and Same Parallels to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Average | Word Problem on Average | Questions on Average
May 19, 25 02:53 PM
In worksheet on average we will solve different types of questions on the concept of average, calculating the average of the given quantities and application of average in different problems. -
8 Times Table | Multiplication Table of 8 | Read Eight Times Table
May 18, 25 04:33 PM
In 8 times table we will memorize the multiplication table. Printable multiplication table is also available for the homeschoolers. 8 × 0 = 0 8 × 1 = 8 8 × 2 = 16 8 × 3 = 24 8 × 4 = 32 8 × 5 = 40 -
How to Find the Average in Math? | What Does Average Mean? |Definition
May 17, 25 04:04 PM
Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities. -
Problems Based on Average | Word Problems |Calculating Arithmetic Mean
May 17, 25 03:47 PM
Here we will learn to solve the three important types of word problems based on average. The questions are mainly based on average or mean, weighted average and average speed. -
Rounding Decimals | How to Round a Decimal? | Rounding off Decimal
May 16, 25 11:13 AM
Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate
Figure on Same Base and between Same Parallels
Parallelograms on Same Base and between Same Parallels
Parallelograms and Rectangles on Same Base and between Same Parallels
Triangle and Parallelogram on Same Base and between Same Parallels
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.