Subscribe to our YouTube channel for the latest videos, updates, and tips.
Parallelograms on Same Base and between Same Parallels
Parallelograms on same base and between same parallels have same area.
|
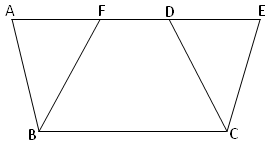
In the adjoining figure, ABCD and BCEF are the two parallelograms on the same base BC and between the parallels BC and AE. |
 |
Therefore, area of parallelogram ABCD = Area of parallelogram BCEF.
Explanation:
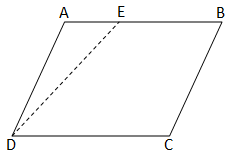
Draw a parallelogram ABCD on a thick sheet of paper or a cardboard sheet.
Now, draw a line segment DE as shown in the figure.
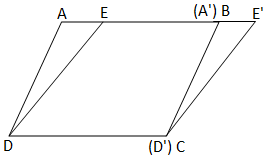
Next, cut a triangle A’D’E’ congruent to triangle ADE in a separate sheet with the help of a tracing paper and place ∆ A’D’E’ in such a way that A’D’ coincides with BC as shown in adjoining figure.
Note that there are two parallelograms ABCD and EE’CD on the same base DC and between the same parallels AE’ and DC. What can you say about their areas?
As ∆ADE ≅ ∆ A’ D’ E’
Therefore Area (ADE) = Area (A’ D’ E’)
Also Area (ABCD) = Area (ADE) + Area (EBCD)
= Area (A’D’E’) + Area (EBCD)
= Area (EE’CD)
So, the two parallelograms are equal in area.
Solved Example:
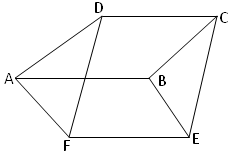
Parallelograms ABCD and ABEF are situated on the opposite sides of AB in such a way that D, A, F are not collinear. Prove that DCEF is a parallelogram, and parallelogram ABCD + parallelogram ABEF = parallelogram DCEF.
Construction: D, F and C, E are joined.
Proof: AB and DC are two opposite sides of parallelogram ABCD,
Therefore, AB ∥ DC and AB = DC
Again, AB and EF are two opposite sides of parallelogram ABEF
Therefore, AB ∥ EF and AB ∥ EF
Therefore, DC ∥ EF and DC = EF
Therefore, DCEF is a parallelogram.
Therefore, ∆ADF and ∆BCE, we get
AD = BC (opposite sides of parallelogram ABCD)
AF = BE (opposite sides of parallelogram ABEF)
And DF = CE (opposite sides of parallelogram CDEF)
Therefore, ∆ADF ≅ ∆BCE (side – side – side)
Therefore, ∆ADF = ∆BCE
Therefore, polygon AFECD - ∆BCE = polygon AFCED - ∆ADF
Parallelogram ABCD + Parallelogram ABEF = Parallelogram DCEF
Figure on Same Base and between Same Parallels
Parallelograms on Same Base and between Same Parallels
Parallelograms and Rectangles on Same Base and between Same Parallels
Triangle and Parallelogram on Same Base and between Same Parallels
Triangle on Same Base and between Same Parallels
8th Grade Math Practice
From Parallelograms on Same Base and between Same Parallels to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Terms Related to Simple Interest | Simple Interest Formula | Principal
Jun 18, 25 02:57 PM
In terms related to simple interest we will learn all the terms related to simple interest. The terms related to simple interest are Interest, Principal, Amount, Simple Interest, Time or period of tim… -
Introduction to Simple Interest | Definition | Formula | Examples
Jun 18, 25 01:50 AM
In simple interest we will learn and identify about the terms like Principal, Time, Rate, Amount, etc. PRINCIPAL (P): The money you deposit or put in the bank is called the PRINCIPAL. -
5th Grade Profit and Loss Percentage Worksheet | Profit and Loss | Ans
Jun 18, 25 01:33 AM
In 5th grade profit and loss percentage worksheet you will get different types of problems on finding the profit or loss percentage when cost price and selling price are given, finding the selling pri… -
Worksheet on Profit and Loss | Word Problem on Profit and Loss | Math
Jun 18, 25 01:29 AM
In worksheet on profit and loss, we can see below there are some different types of questions which we can practice in our homework. -
Calculating Profit Percent and Loss Percent | Profit and Loss Formulas
Jun 15, 25 04:06 PM
In calculating profit percent and loss percent we will learn about the basic concepts of profit and loss. We will recall facts and formula while calculating profit percent and loss percent. Now we wil
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.