sin θ = 0

How to find the general solution of the equation sin θ = 0?

Prove that the general solution of sin θ = 0 is θ = nπ, n ∈ Z

Solution:

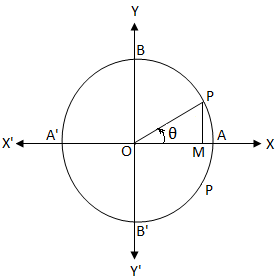
According to the figure, by definition, we have,

Sine function is defined as the ratio of the side opposite divided by the hypotenuse.

sin θ = 0

If we started from A and moves in anticlockwise direction then at the points A, B, A', B' and A, the arc length travelled are 0, \(\frac{π}{2}\), π, \(\frac{3π}{2}\), and 2π.

Therefore, from the above unit circle it is clear that

sin θ = \(\frac{PM}{OP}\)

Now, sin θ = 0

⇒ \(\frac{PM}{OP}\) = 0

⇒ PM = 0.

So when will the sine be equal to zero?

Clearly, if PM = 0 then the final arm OP of the angle θ coincides with OX or, OX'.

Similarly, the final  arm  OP coincides with OX  or OX'  when θ = 0, π, 2π, 3π, 4π, 5π …………….., -π, , -2π, -3π, -4π, -5π ………., i.e., when  θ = 0  or an integral multiples of π i.e., when θ = nπ where n ∈ Z (i.e., n = 0, ± 1, ± 2, ± 3,…….)

Hence, θ = nπ, n ∈ Z is the general solution of the given equation sin θ = 0

1. Find the general solution of the equation sin 2θ = 0

Solution:

sin 2θ = 0

⇒ 2θ = nπ, where, n = 0, ± 1, ± 2, ± 3,……., [Since, we know that θ = nπ, n ∈ Z is the general solution of the given equation sin θ = 0]

⇒ θ = \(\frac{nπ}{2}\), where, n = 0, ± 1, ± 2, ± 3,…….

Therefore, the general solution of the equation sin 2θ = 0 is θ = \(\frac{nπ}{2}\), where, n = 0, ± 1, ± 2, ± 3,…….

2. Find the general solution of the equation sin \(\frac{3x}{2}\) = 0

Solution:

sin \(\frac{3x}{2}\) = 0

⇒ \(\frac{3x}{2}\) = nπ, where, n = 0, ± 1, ± 2, ± 3,…….[Since, we know that θ = nπ, n ∈ Z is the general solution of the given equation sin θ = 0]

⇒ x = \(\frac{2nπ}{3}\), where, n = 0, ± 1, ± 2, ± 3,…….

Therefore, the general solution of the equation sin \(\frac{3x}{2}\) = 0 is θ = \(\frac{2nπ}{3}\), where, n = 0, ± 1, ± 2, ± 3,…….

3. Find the general solution of the equation tan 3x = tan 2x + tan x

Solution:

tan 3x = tan 2x + tan x

⇒ \(\frac{sin    3x}{cos    3x}\) =  \(\frac{sin  2x}{cos  2x}\) + \(\frac{sin  x}{cos  x}\)

⇒ \(\frac{sin  3x}{cos  3x}\) = \(\frac{sin  2x   cos  x  +  cos  2x   sin  x}{cos  2x    cos  x}\)

⇒ cos 3θ sin (2x + x) = sin 3x cos 2x cos x

⇒ cos 3x sin 3x = sin 3x cos 2x cosx

⇒ cos 3x sin 3x - sin 3x cos 2x cos x = 0

⇒ sin 3x [cos (2x + x) - cos 2x cos x] = 0  

⇒ sin 3x . sin 2x sin x = 0

Either either, sin 3x = 0 or, sin 2x = 0 or, sin x = 0

⇒ 3x = nπ or, 2x = nπ or, x = nπ

⇒ x = \(\frac{nπ}{3}\)  …..... (1) or, x = \(\frac{nπ}{2}\)  …..... (2) or, x = nπ …..... (3), where n ∈ I

Clearly, the value of x given in (2) are∶ 0, \(\frac{π}{2}\), π, \(\frac{3π}{2}\), 2π, \(\frac{5π}{2}\) ……………., - \(\frac{π}{2}\),- π, - \(\frac{3π}{2}\) , …………

It is readily seen that the solution x = \(\frac{π}{2}\), \(\frac{3π}{2}\), \(\frac{5π}{2}\)………, - \(\frac{π}{2}\), - \(\frac{3π}{2}\),………
Of the above solution do not satisfy the given equation.

Further  to not  that the  rest  solutions of (2) and the  solution of (3) are contained  in the solutions (1).

Therefore, the general solution of the equation tan 3x = tan 2x + tan x is x = \(\frac{3π}{2}\),, where n ∈ I

4. Find the general solution of the equation sin\(^{2}\) 2x = 0

Solution:

sin\(^{2}\) 2x = 0

sin 2x = 0

⇒ 2x = nπ, where, n = 0, ± 1, ± 2, ± 3,……., [Since, we know that θ = nπ, n ∈ Z is the general solution of the given equation sin θ = 0]

⇒ x = \(\frac{nπ}{2}\), where, n = 0, ± 1, ± 2, ± 3,…….

Therefore, the general solution of the equation sin\(^{2}\) 2x = 0 is x = \(\frac{nπ}{2}\), where, n = 0, ± 1, ± 2, ± 3,…….

● Trigonometric Equations

• General solution of the equation sin x = ½
• General solution of the equation cos x = 1/√2
• General solution of the equation tan x = √3
• General Solution of the Equation sin θ = 0
• General Solution of the Equation cos θ = 0
• General Solution of the Equation tan θ = 0
• General Solution of the Equation sin θ = sin ∝
  
• General Solution of the Equation sin θ = 1
• General Solution of the Equation sin θ = -1
• General Solution of the Equation cos θ = cos ∝
• General Solution of the Equation cos θ = 1
• General Solution of the Equation cos θ = -1
• General Solution of the Equation tan θ = tan ∝
• General Solution of a cos θ + b sin θ = c
• Trigonometric Equation Formula
• Trigonometric Equation using Formula
• General solution of Trigonometric Equation
• Problems on Trigonometric Equation

11 and 12 Grade Math

From sin θ = 0 to HOME PAGE