Subscribe to our YouTube channel for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Problems on Distance Formula
We will discuss here how to solve the problems on distance formula.
The distance between two points A (x1, y1) and B (x2, y2) is given by the formula
AB = √(x1−x2)2+(y1−y2)2
1. If the distance between the points (5, - 2) and (1, a) is 5, find the values of a.
Solution:
We know, the distance between (x1, y1) and (x2, y2)
is √(x1−x2)2+(y1−y2)2
Here, the distance = 5, x1 = 5, x2 = 1, y1 = -2 and y2 = a
Therefore, 5 = √(5−1)2+(−2−a)2
⟹ 25 = 16 + (2 + a)2
⟹ (2 + a)2 = 25 - 16
⟹ (2 + a)2 = 9
Taking square root, 2 + a = ±3
⟹ a = -2 ± 3
⟹ a = 1, -5
2. The co-ordinates of points on the x-axis which are at a distance of 5 units from the point (6, -3).
Solution:
Let the co-ordinates of the point on the x-axis be (x, 0)
Since, distance = √(x2−x1)2+(y2−y1)2
Now taking (6, -3) = (x1, y1) and (x, 0) = (x2, y2), we get
5 = √(x−6)2+(0+3)2
Squaring both sides we get
⟹ 25 = (x – 6)2 + 32
⟹ 25 = x2 – 12x + 36 + 9
⟹ 25 = x2 – 12x + 45
⟹ x2 – 12x + 45 – 25 = 0
⟹ x2 – 12x + 20 = 0
⟹ (x – 2)(x – 10) = 0
⟹ x = 2 or x = 10
Therefore, the required points on the x-axis are (2, 0) and (10, 0).
3. Which point on the y-axis is equidistance from the points (12, 3) and (-5, 10)?
Solution:
Let the required point on the y-axis (0, y).
Given (0, y) is equidistance from (12, 3) and (-5, 10)
i.e., distance between (0, y) and (12, 3) = distance between (0, y) and (-5, 10)
⟹ √(12−0)2+(3−y)2 = √(−5−0)2+(10−y)2
⟹ 144 + 9 + y2 – 6y = 25 + 100 + y2 – 20y
⟹ 14y = -28
⟹ y = -2
Therefore, the required point on the y-axis = (0, -2)
4. Find the values of a such that PQ = QR, where P, Q and R are the points whose coordinates are (6, - 1), (1, 3) and (a, 8) respectively.
Solution:
PQ = √(6−1)2+(−1−3)2
= √52+(−4)2
= √25+16
= √41
QR = √(1−a)2+(3−8)2
= √(1−a)2+(−5)2
= √(1−a)2+25
Therefore, PQ = QR
⟹ √41 = √(1−a)2+25
⟹ 41 = (1 - a)2 + 25
⟹ (1 - a)2 = 41 - 25
⟹ (1 - a)2 = 16
⟹ 1 - a = ±4
⟹ a = 1 ±4
⟹ a = -3, 5
5. Find the points on the y-axis, each of which is at a distance of 13 units from the point (-5, 7).
Solution:
Let A (-5, 7) be the given point and let P (0, y) be the required point on the y-axis. Then,
PA = 13 units
⟹ PA2 = 169
⟹ (0 + 5)2 + (y - 7)2 = 169
⟹ 25 + y2 - 14y + 49 = 169
⟹ y2 – 14y + 74 = 169
⟹ y2 – 14y – 95 = 0
⟹ (y - 19)(y + 5) = 0
⟹ y – 19 = 0 or, y + 5 = 0
⟹ y = 19 or, y = -5
Hence, the required points are (0, 19) and (0, -5)
● Distance and Section Formulae
- Distance Formula
- Distance Properties in some Geometrical Figures
- Conditions of Collinearity of Three Points
- Problems on Distance Formula
- Distance of a Point from the Origin
- Distance Formula in Geometry
- Section Formula
- Midpoint Formula
- Centroid of a Triangle
- Worksheet on Distance Formula
- Worksheet on Collinearity of Three Points
- Worksheet on Finding the Centroid of a Triangle
- Worksheet on Section Formula
10th Grade Math
From Problems on Distance Formula to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
5th Grade Circle Worksheet | Free Worksheet with Answer |Practice Math
Jul 11, 25 02:14 PM
In 5th Grade Circle Worksheet you will get different types of questions on parts of a circle, relation between radius and diameter, interior of a circle, exterior of a circle and construction of circl… -
Construction of a Circle | Working Rules | Step-by-step Explanation |
Jul 09, 25 01:29 AM
Construction of a Circle when the length of its Radius is given. Working Rules | Step I: Open the compass such that its pointer be put on initial point (i.e. O) of ruler / scale and the pencil-end be… -
Combination of Addition and Subtraction | Mixed Addition & Subtraction
Jul 08, 25 02:32 PM
We will discuss here about the combination of addition and subtraction. The rules which can be used to solve the sums involving addition (+) and subtraction (-) together are: I: First add -
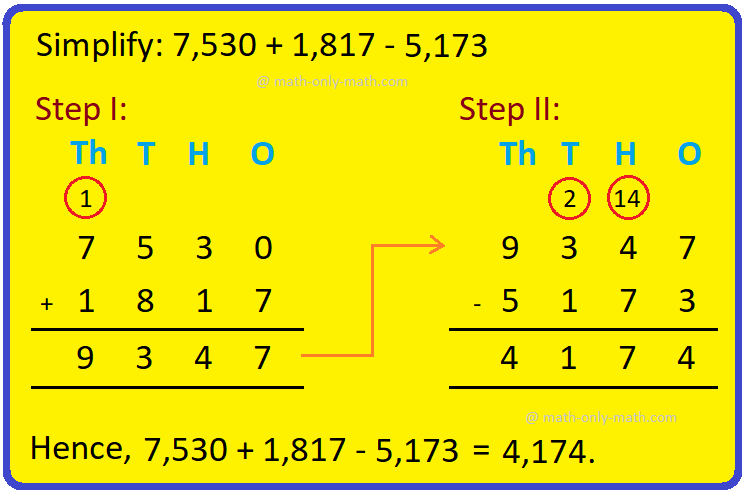
Addition & Subtraction Together |Combination of addition & subtraction
Jul 08, 25 02:23 PM
We will solve the different types of problems involving addition and subtraction together. To show the problem involving both addition and subtraction, we first group all the numbers with ‘+’ and… -
5th Grade Circle | Radius, Interior and Exterior of a Circle|Worksheet
Jul 08, 25 09:55 AM
A circle is the set of all those point in a plane whose distance from a fixed point remains constant. The fixed point is called the centre of the circle and the constant distance is known

New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.